Atención: para poder examinar las sobrepresiones intersticiales, primero se deben asignar los datos adicionales en características geotécnicas.
Presiones intersticiales post sismo Para examinar las sobrepresiones intersticiales después de un sismo, asignar un valor igual a cero a los coeficientes sísmicos horizontales y verticales, y un valor diferente de cero a la aceleración sísmica.
|
Resistencia al corte en condiciones de carga sísmica.
Ante la falta de determinaciones experimentales adecuadas obtenidas con pruebas cíclicas de laboratorio, la reducción de resistencia al corte en condiciones de carga sísmica se puede estimar con base en relaciones empíricas, como se indica a continuación, haciendo referencia al caso de análisis en términos eficaces o en términos de tensiones totales.
Análisis en condiciones de tensiones eficaces.
El incremento de presión intersticial se debe evaluar, en caso de terrenos saturados, si la deformación de corte debida a la acción sísmica es superior al valor de la deformación volumétrica límite, γv. En terrenos parcialmente saturados, las presión intersticial aumenta con la aplicación de la solicitación sísmica, pero se mantiene generalmente inferior a la presión atmosférica; en ese caso las presiones intersticiales pueden asumir valor nulo en todo el período de la aplicación de la carga (σ’=s) y los análisis se pueden llevar a cabo utilizando las características de resistencia determinadas con ensayos drenados efectuados en muestras previamente saturadas del mismo material. Para calcular Δu conviene distinguir el comportamiento de los suelos según su naturaleza, cohesiva o incoherente.
Suelos cohesivos
En terrenos cohesivos, el incremento de presión intersticial Δu, a una cierta profundidad, se puede estimar con la siguiente relación empírica (Matsui et al., 1980):
![]()
Donde σ’0 es el valor inicial de la presión promedio efectiva a la profundidad considerada, γc,max es la deformación de corte máxima alcanzada durante el sismo y β=0.45 es un coeficiente experimental. La deformación límite volumétrica γv, determinable con ensayos cíclicos de laboratorio, se puede calcular como primera aproximación mediante la relación:
![]()
En la cual OCR es el grado de sobreconsolidación, A y B son coeficientes experimentales que, en ausencia de una determinación directa, se pueden fijar en función del índice de plasticidad:
Ip (%) |
A |
B |
20 |
0.4 10-3 |
0.6 10-3 |
40 |
1.2 10-3 |
1.1 10-3 |
55 |
2.5 10-3 |
1.2 10-3 |
Valores recomendados para los coeficientes A y B
El valor de γc,max relativo a la profundidad considerada se puede determinar analizando la respuesta sísmica local. En alternativa, se determina preliminarmente el valor de τmax mediante la relación empírica:
![]()
Donde amax, expresada en g, es la aceleración pico en el plano del terreno en la vertical del punto considerado; g es la aceleración de gravedad; σv es la tensión vertical total; rd es un coeficiente reductor que tiene en cuenta la acción sísmica a la profundidad de interés que considera la deformabilidad del subsuelo. El coeficiente rd se puede estimar, como primera aproximación, con la siguiente expresión:
![]()
Donde z es la profundidad en el punto considerado. La máxima deformación de corte provocada por el sismo se obtiene por lo tanto con:
![]()
Donde el módulo de corte G se puede determinar, por iteración, con la curva (G-γ) obtenida con ensayos de laboratorio.
Suelos granulares.
En terrenos granulares, el incremento de presión intersticial generado por la solicitación sísmica se puede estimar con la siguiente relación empírica (Seed & Booker, 1997):
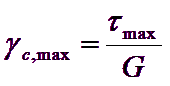
Donde ΔuN un es el incremento de presión intersticial al cabo de N ciclos de carga, σ’0 el valor inicial de la presión promedio efectiva a la profundidad considerada, N es el número de ciclos de carga de amplitud constante equivalente al sismo y NL es el número de ciclos necesarios para que se produzca la licuefacción. La constante experimental a se puede estimar con la relación de Fardis & Veneziano (1981) en función de la densidad relativa Dr (en fracción):
![]()
El término εq tiene distribución log-normal con valor promedio unitario y varianza igual a 0.1. Para determinar el número de ciclos N que aparece en una de las relaciones precedentes, es necesario aproximar el historial de deformaciones por corte irregular debidas al sismo con una solicitación cíclica equivalente de amplitud constante (τeq) ey número de ciclos equivalente (Neq) siguiendo una de los numerosos procedimientos presentes en las bibliografías. Utilizando por ejemplo el procedimiento que propone Biondi et al. (2004) se obtiene:
![]()
![]()
En la primera de estas ecuaciones τmax representa la solicitación de corte inducida por el sismo a la profundidad considerada, cuyo valor se puede estimar analizando la respuesta sísmica local o, en primera aproximación, con la relación utilizada en la sección de los terrenos cohesivos. En la segunda ecuación los términos tienen los siguientes significados:
-Ia : es la intensidad de Arias (m/s)
-v0 : es la intensidad de las intersecciones con el eje del tiempo del acelerograma (s-1)
-TD : es la duración del acelerograma definida por Trifunac y Brady (s)
La intensidad de Arias se define con la siguiente fórmula:
![]()
Los otros símbolos, o sea α - c - γ - δ - ε, son constantes para las cuales se recomiendan los siguientes valores:
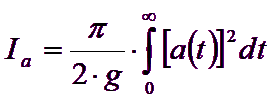
Para determinar el valor de NL se puede hacer referencia a métodos basados en interpolaciones de tipo gráfico, o eventualmente se pueden utilizar los resultados de ensayos triaxiales cíclicos o de corte simple cíclico.
© GeoStru Software