Il Metodo della Spirale Logaritmica, introdotto da Taylor nel 1937, è una tecnica analitica impiegata nell'analisi di stabilità dei pendii.
Principi Fondamentali e Vantaggi
•In questo metodo si supera la difficoltà di dover assumere arbitrariamente la distribuzione delle forze lungo la superficie di rottura. Questo è un problema comune in altri metodi di equilibrio limite, come il metodo del cerchio di attrito o il metodo delle strisce.
•La proprietà chiave della spirale logaritmica risiede nel fatto che la risultante delle forze normali e delle forze di attrito passa sempre attraverso l'origine della spirale.
•Di conseguenza, quando si calcola il momento rispetto all'origine della spirale, l'effetto combinato delle forze normali e di attrito è nullo. Ciò semplifica notevolmente il calcolo, poiché rimangono da considerare solo i momenti dovuti al peso del terreno e alla coesione.
•Questa caratteristica lo rende un "punto di riferimento" (yardstick) per verificare l'accuratezza di altri metodi di analisi, dato che soddisfa l'equilibrio dei momenti senza ulteriori assunzioni al di fuori della forma a spirale logaritmica della superficie di rottura.
Equazione della Spirale Logaritmica
L'equazione di una spirale logaritmica in coordinate polari è espressa come: r = ro e(θ * tan φ)
Dove:
•r è il raggio dall'origine alla spirale logaritmica.
• ro è il raggio iniziale.
• θ è l'angolo (in radianti) tra il raggio iniziale e il raggio r. La lunghezza del raggio aumenta se θ è misurato in senso orario; diminuisce se è misurato in senso antiorario (θ negativo).
• φ è l'angolo di attrito interno del terreno. La forma della spirale logaritmica è controllata da φ. Una linea normale alla spirale logaritmica forma sempre un angolo φ con la linea radiale.
L'origine della spirale logaritmica è localizzata tramite due angoli arbitrari t e z
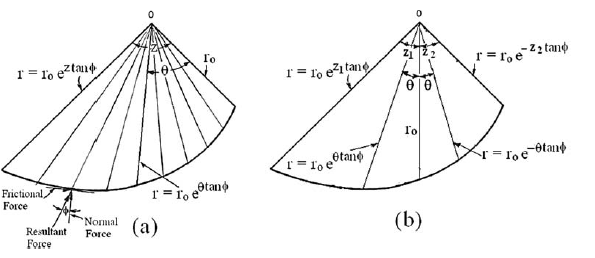
Caratteristiche della spirale logaritmica
Nell'utilizzo del metodo del cerchio di attrito o del metodo delle strisce, la distribuzione delle forze lungo l'arco di rottura o sui lati di una striscia deve essere assunta in modo arbitrario. Questa difficoltà può essere superata se come superficie di rottura si utilizza una spirale logaritmica.
A prescindere dall'intensità delle forze normali sulla superficie di rottura, la proprietà della spirale logaritmica è tale che la risultante delle forze normali e di quelle d'attrito passa sempre per l'origine della spirale. Di conseguenza, quando si calcola il momento rispetto all'origine, l'effetto combinato delle forze normali e d'attrito è nullo, e devono essere considerati soltanto i momenti dovuti al peso e alla coesione. Questo metodo della spirale logaritmica fu proposto per la prima volta da Taylor (1937) per l'analisi di stabilità.
Come impostare una superficie di scorrimento a spirale logaritmica in Slope
1.Definire la geometria della sezione e la sua stratigrafia
2.Definire le coordinate dei vertici superiore, inferiore e il numero di righe della superficie di scorrimento. È possibile definire questi parametri per via grafica passando ad una superficie circolare, disegnare la maglia dei centri e poi ritornare a superfcie generica: il software memorizzerà i dati.
3.Definire le coordinate del punto di passaggio delle spirali logaritmiche: va inserito un punto consono al profilo di sezione.
4.Premere Genera, eventualmente impostare "Adatta la spirale al profilo" per eliminare i tratti di spirale che ricadono al di fuori della sezione
5.Eventualmente infittire il passo del numero dei punti delle spirali, il numero righe, colonne della maglia dei centri o le coordinate di quest'ultima
6.Effettuare il calcolo
© GeoStru