Liang e Zeng (2002) hanno effettuato una serie di analisi parametriche su un modello bidimensionale sviluppato con codice agli elementi finiti, che riproduce il caso di pali immersi in un terreno in movimento (drilled shafts). Il modello bidimensionale riproduce un striscia di terreno di spessore unitario e ipotizza che il fenomeno avvenga in condizioni di deformazione piana nella direzione parallela all’asse dei pali. Il modello è stato utilizzato per indagare l’influenza sulla formazione dell’effetto arco di alcuni parametri come l’interasse fra i pali, il diametro e la forma dei pali, e le proprietà meccaniche del terreno. Gli autori individuano nel rapporto tra l’interasse e il diametro dei i pali (s/d) il parametro adimensionale determinante per la formazione dell’effetto arco.
Il problema risulta essere staticamente indeterminato, con grado di indeterminatezza pari a (8n-4), ma nonostante ciò è possibile ottenere una soluzione riducendo il numero delle incognite e assumendo quindi delle ipotesi semplificative, in modo da rendere determinato il problema.
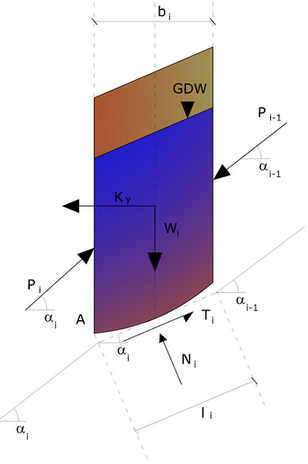
Azioni sul concio i-esimo secondo le ipotesi di calcolo di Zeng e Liang
Le assunzioni che rendono il problema determinato sono:
-Ky sono assunte orizzontali per ridurre il numero totale delle incognite da (n-1) a (7n-3);
-Le forze normali alla base della striscia agiscono nel punto medio, riducendo le incognite da n a (6n-3);
-La posizione delle spinte laterali è ad un terzo dell’altezza media dell’inter-striscia e riduce le incognite da (n-1) a (5n-2);
-Le forze (Pi-1) e Pi si assumono parallele all’inclinazione della base della striscia (αi), riducendo il numero di incognite da (n-1) a (4n-1);
-Si assume un’unica costante di snervamento per tutte le strisce, riducendo le incognite da (n) a (3n-1);
Il numero totale di incognite quindi è ridotto a (3n), da calcolare utilizzando il fattore di trasferimento di carico. Inoltre si deve tener presente che la forza di stabilizzazione trasmessa sul terreno a valle dei pali risulta ridotta di una quantità R, chiamato fattore di riduzione, calcolabile come:
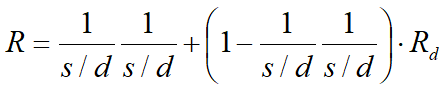
Il fattore R dipende quindi dal rapporto fra l’interasse presente fra i pali e il diametro dei pali stessi e dal fattore Rd che tiene conto dell’effetto arco.
© GeoStru