Metoda echilibrului limită constă în studiul echilibrului unui corp rigid, constituit din taluz și dintr-o suprafață de alunecare de formă oarecare (linie dreaptă, arc de cerc, spirală logaritmică, etc.), de la acest tip de echilibru se calculează tensiunile la forfecare (τ) și se compară cu rezistența disponibilă (τf) calculată conform criteriului de cedare Coulomb; din această comparație ia naștere prima indicație asupra stabilității prin factorul de siguranță.
F =τf /τ
Dintre metodele de echilibru limită, unele iau în considerare echilibrul global al corpului rigid (Culman), altele, din cauza neomogeneizații, divid corpul în fâsii considerând echilibrul fiecăreia (Fellenius, Bishop, Janbu, etc).
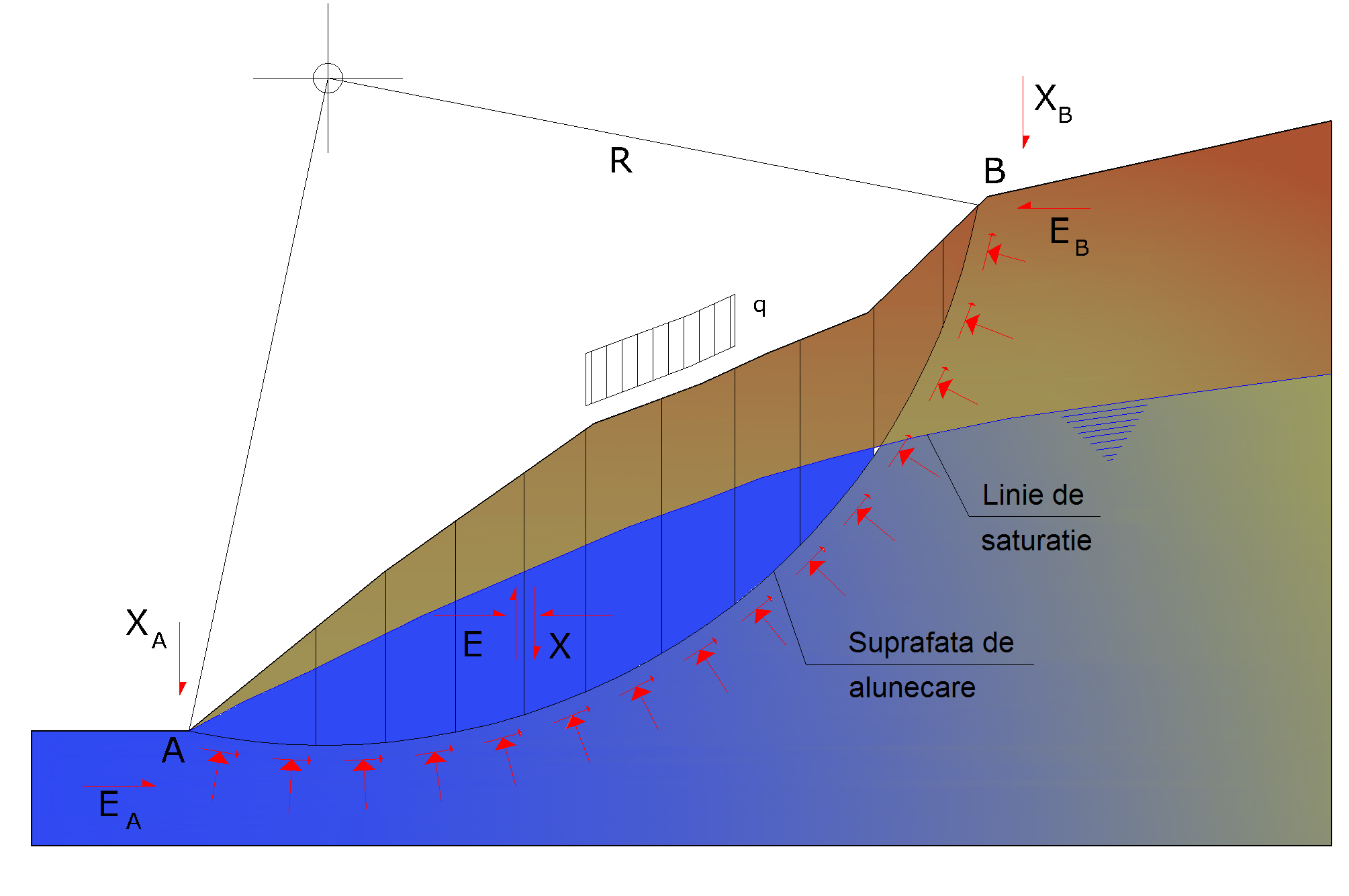
Reprezentarea unei secțiuni de calcul a unui versant
Metoda fâșiilor
Masa supusă alunecării este divizată într-un număr convenabil de fâșii. Dacă numărul acestora este egal cu n, problema prezintă următoarele necunoscute:
•n valori ale forțelor normale Ni care acționează asupra bazei fiecărei fâșii;
•n valori ale forțelor de forfecare la baza fâșiei Ti;
•(n-1) forțe normale Ei care acționează pe interfața fâșiilor;
•(n-1) forțe tangențiale Xi care acționează pe interfața fâșiilor;
•n valori ale coordonatei "a" care identifică punctul de aplicare a Ei;
•(n-1) valori ale coordonatei care identifică punctul de aplicare a Xi;
•o necunoscută constituită din factorul de siguranță F.
În total sunt (6n-2) necunoscute.
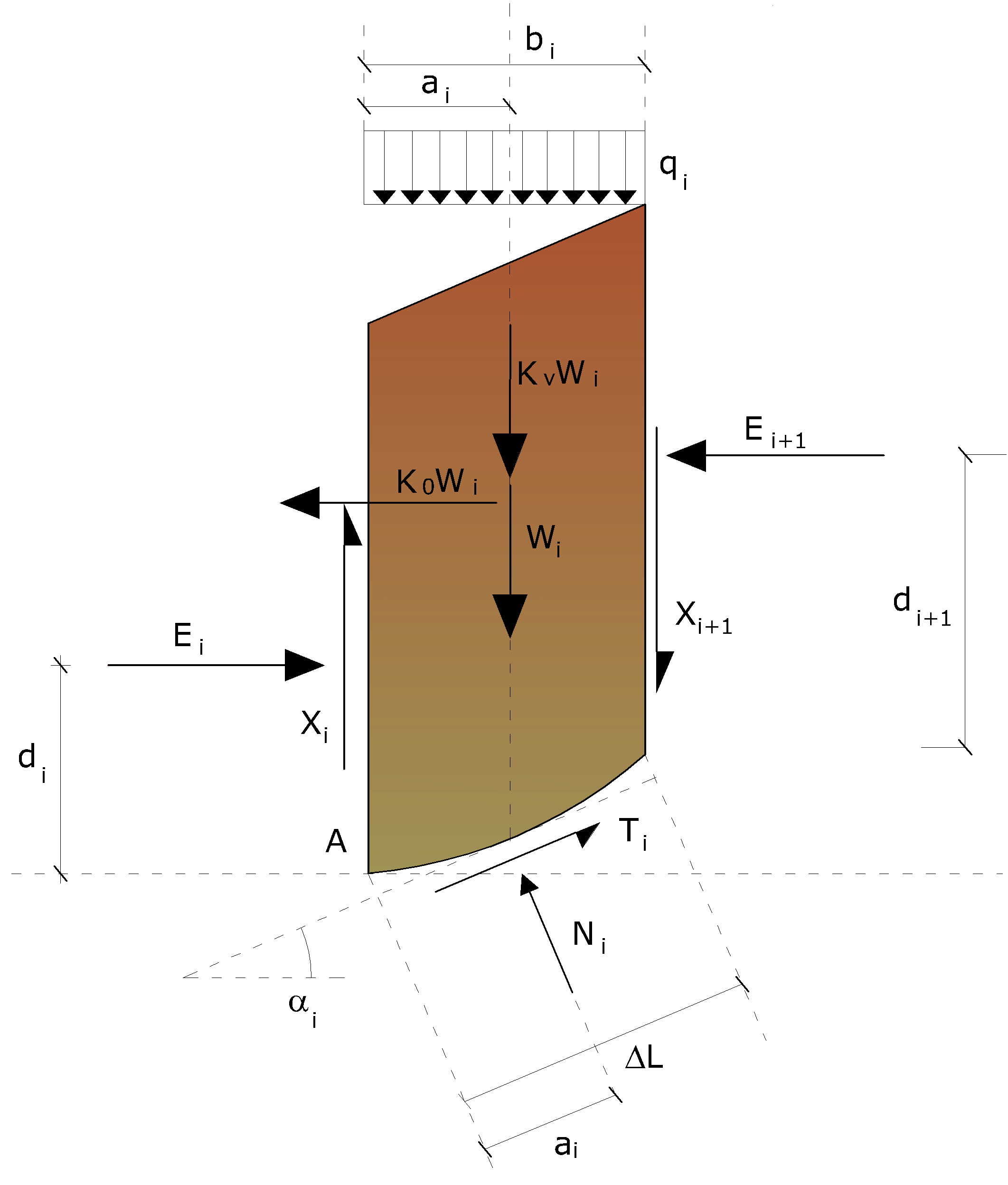
Acțiuni asupra fâșiei
în timp ce ecuațiile disponibile sunt:
•Ecuații de echilibru ale momentelor n
•Ecuații de echilibru la deplasare verticală n
•Ecuații de echilibru la deplasare orizontală n
•Ecuații care se referă la criteriul de cedare n
Numărul total de ecuații 4n
Problema este static nedeterminată iar gradul de nedeterminare este de:
i = (6n-2)-(4n) = 2n-2.
Gradul de nedeterminare se reduce ulterior cu (n-2) întrucât se presupune că Ni este aplicat în punctul mediu al fâșiei, echivalent cu a presupune că tensiunile normale totale sunt uniform distribuite.
Diversele metode care se bazează pe teoria echilibrului limită se diferențiază prin modul în care se elimină (n-2) nedeterminate.
© GeoStru