<< Click to Display Table of Contents >> Navigation:  SLOPE > Suprapresiuni interstițiale

 

Rezistenta la forfecare în condiții de sarcină seismică.

În lipsa unor determinări experimentale adecvate, obținute din încercări ciclice de laborator, reducerea rezistentei de forfecare în condiții de sarcină seismică poate fi calculată folosind relații empirice de citire, după cum este indicat în paragrafele de mai jos, cu referire la cazul analizelor conduse în termeni de tensiuni efective sau de tensiuni totale.

 

Analiza în condiții de tensiuni efective.

Incrementul presiunii interstițiale trebuie calculat în cazul terenurilor saturate dacă deformarea la forfecare indusă de acțiunea seismică este superioară valorii deformării pragului volumetric, γv. În terenuri parțial saturate, presiunea interstițiala crește în timpul aplicării solicitării seismice, dar se menține în general inferioară presiunii atmosferice; în acest caz poate fi luată o valoare nulă a presiunilor interstițiale pentru toată perioada de aplicare a sarcinii (σ’=s) iar dacă analizele pot fi realizate utilizând caracterisiticile de rezistență determinate în încercări drenate realizate pe specimene saturate ale aceluiași material. Pentru calculul lui Du trebuie făcută distincție între comportamentele terenurilor în funcție de natura lor diferită, coezivă sau necoezivă.

 

Terenuri coezive.

Pentru terenurile coezive, incrementul de presiune interstițială Δu, la o anumită adâncime, poate fi calculat cu ajutorul următoarei relații empirice (Matsui et al., 1980):

Unde σ’0 este valoarea inițială a presiunii medii efective la adâncimea considerată, γc,max este deformarea de forfecare maximă atinsă în timpul seismului iar β=0.45 este un coeficient experimental. Deformarea pragului volumetric γv, determinabil cu încercări ciclice de laborator, poate fi calculat într-o primă aproximare cu ajutorul formulei:

În care OCR este gradul de supraconsolidare, A și B sunt coeficienți experimentali care, în absenta unei determinări directe, pot fi calculați în funcție de indicele de plasticitate:

 

Valori sugerate pentru coeficienții A și B

 

Valoarea lui γc,max relativ la adâncimea considerată poate fi determinat prin intermediul unei analize a răspunsului seismic local. Altfel, se determină preliminar valoarea lui τmax cu ajutorul formulei empirice:

 

Unde amax, exprimată în g, este accelerația maximă la nivelul terenului pe verticala relativă punctului considerat; g este accelerația gravitațională; σv este tensiunea verticală totală; rd este un coeficient reductiv ce ține cont de acțiunea seismică la adâncimea de interes care aduce în discuție deformabilitatea subsolului. Coeficientul rd poate fi calculat, ca primă aproximare, cu expresia de mai jos:

Unde z este adâncimea în punctul considerat. Deformarea maximă de forfecare indusă de seism se calculează deci cu formula:

Unde modulul de forfecare G poate fi determinat, iterativ, de curba (G-γ) obținută din încercări de laborator.

 

Terenuri granulare.

În terenurile granulare incrementul presiunii interstițiale generat de solicitarea seismică poate fi calculat cu următoarea formulă empirică (Seed & Booker, 1997):

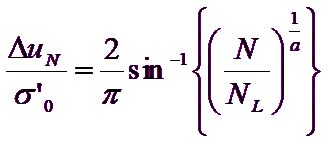
Unde ΔuN este incrementul de presiune interstițială după N cicluri de sarcină, σ’0 este valoarea inițială a presiunii medii efective la adâncimea considerată, N este numărul de cicluri de sarcină de amplitudine constantă echivalentă seismului iar NL este numărul de cicluri de sarcină necesare pentru producerea lichefierii în teren. Constanta experimentală a poate fi calculată cu relația propusă de Fardis & Veneziano (1981) în funcție de densitatea relativă Dr (în fracție):

Termenul εq are distribuție log-normală cu valoare medie unitară și variație egală cu 0.1. Pentru determinarea numărului de cicluri N ce apare în una dintre relațiile anterioare este necesară aproximarea deformărilor de forfecare neregulate induse de cutremur cu o solicitare ciclică echivalență de amplitudine constantă (τeq) si număr de cicluri echivalent (Neq) urmând una dintre numeroasele proceduri prezente în literatură. Utilizând de exemplu procedura propusă de Biondi et al. (2004) se obține:

În prima dintre ecuațiile precedente τmax reprezintă solicitarea de forfecare maximă indusă de teren la adâncimea considerată, a cărei valori poate fi calculat cu ajutorul unei analize a răspunsului seismic local sau, la o primă aproximare, cu ajutorul unei formule utilizate în paragraful referitor la terenuri coezive. În a doua ecuație din cele precedente diverșii termeni au următoarele semnificații:

 

-Ia                intensitatea lui di Arias (m/s);

-v0        intensitatea intersecțiilor cu axa timpilor accelerogramei (s-1);

-TD        durata accelerogramei definită de Trifunac și Brady (s);

 

Intensitatea lui Arias este definită prin formula de mai jos:

Celelalte simboluri care apar, α -β -γ - δ - ε, sunt constante pentru care se sugerează valorile:

 

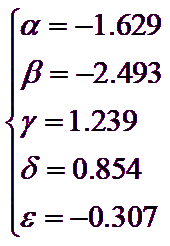
Pentru determinarea valorii lui NL se poate face referire la metodele ce se bazează pe interpolări de tip grafic sau eventual pe utilizarea rezultatelor din încercări triaxiale ciclice sau de forfecare simplă ciclică.

 

 

©  GeoStru