La verifica a scorrimento, nel caso di pereti rinforzate con la tecnica del Soil Nailing, può essere considerata come un caso particolare della verifica di stabilità globale, che può verificarsi quando al di sotto del blocco rinforzato giace uno strato debole. In accordo alle linee guida americane FHWA-NHI-14-007, la verifica a scorrimento può essere eseguita con riferimento al meccanismo indicato in Fig. 6.
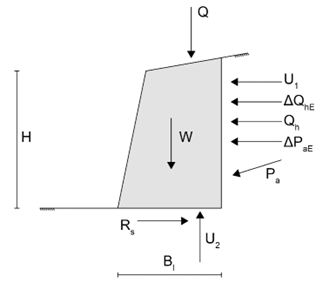
Fig. 6 – Meccanismo di rottura utilizzato per eseguire la verifica nei confronti dello scorrimento, in accordo alle linee guida americane FHWA-NHI-14-007.
Le azioni indicate nello schema in Fig. 6 sono le seguenti:
Pa: spinta del terreno dovuta al proprio peso, in termini di tensioni efficaci, in condizioni statiche
ΔPaE: incremento della spinta del terreno in termini di tensioni efficaci per effetto del sisma
W: peso del cuneo potenzialmente instabile
Q: risultante dei carichi applicati sul piano campagna
Qh: risultante delle tensioni orizzontali agenti sulla parete verticale, per effetto dei carichi applicati sul piano campagna, in condizioni statiche
ΔQhE: incremento di Qh per effetto del sisma
U1: risultante delle pressioni neutre agenti sulla parete verticale
U2: sottospinta dell’acqua
Rs: resistenza nei confronti dello scorrimento
È necessario notare che la posizione in cui tali forze sono rappresentate in Fig. 6 è del tutto indicativa, poiché la verifica viene eseguita utilizzando le equazioni di equilibrio nella direzione orizzontale e verticale, mentre l’equilibrio alla rotazione non viene imposto; pertanto, i bracci non entrano in gioco. Il peso W viene calcolato moltiplicando il peso dell’unità di volume del blocco per l’area corrispondente, mentre Q viene calcolato come la somma delle risultanti di tutti i carichi nella direzione verticale applicati sul piano campagna nell’ambito della larghezza Bl. Qh viene calcolata come la risultante delle tensioni orizzontali dovute ai carichi applicati sul piano campagna, con riferimento alla teoria del semispazio elastico. Tale valore si riferisce alla condizione statica, ed è quindi funzione del coefficiente di spinta attiva Ka. Per il calcolo di ΔQhE viene utilizzata la seguente equazione:
|
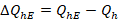 |
(17) |
In cui QhE è l’analogo di Qh, riferito però alla condizione pseudostatica, ed è calcolato quindi in funzione del coefficiente di spinta attiva KaE. Le altre forze vengono calcolate utilizzando le seguenti equazioni:
|
|
(18) |
Tale equazione vale nel caso di terreno omogeneo ed asciutto. In presenza di falda, l’equazione viene modificata tenendo conto opportunamente del peso dell’unità di volume alleggerito per le porzioni di terreno al di sotto del livello di falda. Il valore di H1 rappresenta invece l’altezza della parete verticale interna del cuneo potenzialmente instabile. Inoltre:
|
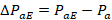 |
(19) |
In cui PaE è analogo a Pa con la differenza che il calcolo viene eseguito utilizzando il coefficiente KaE al posto di Ka. Analogamente alle verifiche esposte in precedenza, Pa e ΔPaE vengono considerati separatamente (al posto di considerare direttamente PaE), in modo tale da poter utilizzare diversi coefficienti amplificativi nel caso in cui si voglia utilizzare un approccio di normativa. La risultante delle pressioni neutre U1 viene calcolata mediante la seguente equazione:
|
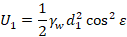 |
(20) |
In cui d1 è la porzione di H1 al di sotto della falda. Tale equazione vale nell’ipotesi che, in presenza di piano campagna inclinato, la falda sia parallela al piano campagna e che si abbia un moto di filtrazione parallelo ad esso. La sottospinta U2 assume invece la seguente espressione:
|
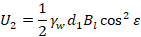 |
(21) |
La resistenza nei confronti dello scorrimento è invece pari a:
|
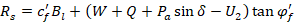 |
(22) |
In cui cf' e φf' sono rispettivamente coesione ed angolo di resistenza al taglio del terreno di fondazione.
La verifica nei confronti dello scorrimento consiste nell’assicurarsi che il relativo coefficiente di sicurezza sia maggiore dell’unità. Tale coefficiente è definito nel seguente modo:
|
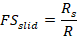 |
(23) |
In cui
|
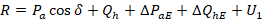 |
(24) |
Infine, è necessario tenere presente che la verifica viene eseguita con riferimento ad un cuneo potenzialmente instabile di larghezza pari a Bl. Tale larghezza può essere assunta oppure calcolata. In quest’ultimo caso, nel seguito vengono considerate le seguenti opzioni per il calcolo di Bl:
|
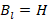 |
(25) |
|
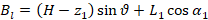 |
(26) |
In tale equazione, z1 rappresenta la profondità del primo chiodo rispetto alla testa della parete, mentre L1 ed α1 sono rispettivamente la lunghezza e l’inclinazione del medesimo chiodo.
©GeoStru