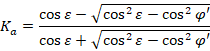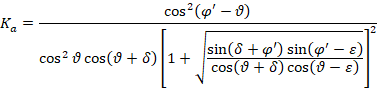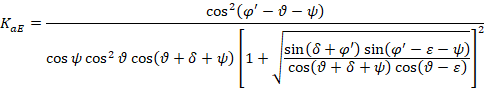Forța de tracțiune acționând asupra fiecărui cui, Fi, poate fi evaluată prin următoarea expresie, valabilă în prezența unui nivel freatic, în condiții pseudo-statice și sol omogen:
|
|
(4) |
În care termenii individuali iau următoarele expresii:
kn: coeficient redus
σa,i': tensiune activă efectivă la adâncimea medie a zonei de influență a cuiului i
Sv,i: distanța verticală între cuie; definește și grosimea zonei de influență a cuiului i
Sh: distanța orizontală între cuiuri
αi: înclinare, în raport cu direcția orizontală, a cuiului i
∆σaE,i':creșterea tensiunii active efectivă la adâncimea medie a zonei de influență a cuiului i datorată cutremurului
ui: presiune neutră la adâncimea medie a zonei de influență a cuiului i
Tensiunea activă efectivă este calculată în funcție de coeficientul de presiune activă, Ka, a tensiunii active verticale acționând la adâncimea punctului considerat, σv,i' a oricărei încărcături q aplicate pe terasament și a coeziunii efectivă, c':"
|
|
(5) |
În continuare, coeficientul de presiune activă este calculat folosind următoarele teorii:
Teoria lui Rankine:
|
|
(6) |
Teoria lui Coulomb
În care δ reprezintă unghiul de frecare între perete și sol, în timp ce θ, definit în Fig. 2, trebuie utilizat în Eq. 7 cu semn negativ. Toți ceilalți parametri au fost introduse anterior. În ceea ce privește creșterea tensiunii datorată cutremurului, aceasta este calculată în modul următor:
|
|
(7) |
În care δ reprezintă unghiul de frecare între perete și sol, în timp ce θ, definit în Fig. 2, trebuie utilizat în Eq. 7 cu semn negativ. Toți ceilalți parametri au fost introduși anterior. În ceea ce privește creșterea tensiunii datorată cutremurului, aceasta este calculată în modul următor:
|
|
(8) |
În care σaE,i' reprezintă tensiunea activă eficace la adâncimea medie a zonei de influență a cuiului i datorită cutremurului:
|
|
(9) |
În care KaE este coeficientul de presiune activă în condiții seismice, calculat în continuare folosind teoria Mononobe-Okabe:
|
|
(10) |
În care:
|
|
(11) |
Este important de observat că în Ec. 4, suma dintre primul și al doilea termen ar putea fi înlocuită utilizând Ec. 8. Cu toate acestea, s-a preferat menținerea separată a contribuției statice de la creșterea cauzată de cutremur, deoarece în cazul în care se dorește aplicarea unei abordări normative, este posibil să se înmulțească cei doi termeni cu coeficienți diferiți.
În cazul unei analize efectuate în condiții statice, al doilea termen al Ec. 4 se anulează, în timp ce în cazul unui teren uscat se anulează al treilea termen și în primul termen tensiunea activă eficace coincide cu cea totală.
În cazul cel mai general, în care terenul este stratificat, în funcție de poziția grosimii de influență a fiecărui cui în raport cu straturile de teren, sunt posibile cele patru cazuri diferite indicate în Fig. 5."
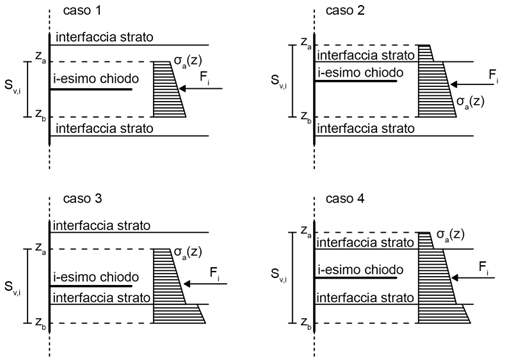
Fig. 5 - Posibile distribuții ale tensiunii orizontale totale, σa (z), în funcție de adâncime, în funcție de poziție, grosimea fiecărui cui în raport cu straturile de teren.
Cu referire la fiecare dintre aceste cazuri, Fig. 5 arată evoluția cu adâncimea a tensiunii orizontale totale, σa (z), care este caracterizată de un salt și o schimbare de înclinare în corespondență cu interfețele dintre straturi. Pentru astfel de situații, este convenabil să se calculeze forța de tracțiune acționând asupra fiecărui element de armare ca rezultanta a distribuției tensiunilor orizontale:
|
|
(12) |
În care za și zb sunt adâncimile care definesc începutul și sfârșitul zonei de influență a cuiului i. În condiții pseudo-statice, în Ec. 12 este necesar să se adauge termenul datorat creșterii tensiunii datorită cutremurului, utilizând aceeași logică văzută în cazul terenului omogen.
© Geostru