Por filtración se entiende el fenómeno físico con el cual se da el pasaje del agua, a través de un medio poroso, de una zona con una determinada energía a otra con energía menor.
La energía se puede expresar como la suma de la energía cinética ligada a la velocidad del fluido, de la potencial que depende de la posición del punto y de la de presión del líquido en el mismo punto. Puesto que la velocidad de filtración es siempre muy pequeña, se puede obviar el término cinético.
Al estudiar la filtración del agua se pueden presentar ciertos problemas, ya sean de flujo permanente que de flujo variable:
En cuanto a la presión del agua, la cual juega un papel importante en la mayoría de los problemas de estabilidad, se recuerda que cuando el movimiento es permanente la misma es constante en el tiempo; mientras que con movimiento variable la presión del agua está en función del tiempo y por lo tanto puede aumentar o disminuir.
Con referencia a la cantidad de agua que debido al fenómeno de la filtración atraviesa una cierta zona, se recuerda que en régimen permanente la cantidad de agua que entra es igual a la cantidad que sale, mientras que en régimen variable no existe igualdad y la diferencia representa el volumen de agua que acumula o que expulsa el terreno en el intervalo de tiempo considerado.
En el fenómeno de consolidación, la cual es una condición particular del régimen variable, entra también en juego la compresibilidad del terreno. En condiciones permanentes la zona de terreno donde se da la filtración (en el esquema de representación adoptado) tiene dos tipos de confines: uno es el lugar donde se conoce la carga de agua, que se define como confín o condición límite del potencial, mientras que el otro es un contorno de materiales impermeables, como roca impermeable, arcilla, etc. que delimita el estrato donde se da la filtración y se define como confín o condición límite del flujo de agua. Se pueden recordar como ejemplo las condiciones de flujo de agua en el ensayo de permeabilidad con carga constante. En este ensayo evidentemente los confines del potencial son las superficies de entrada y de salida del agua de la muestra de suelo. Debido a que las paredes del contenedor son impermeables, el flujo es paralelo al mismo y la pared constituye el confín del flujo del agua:
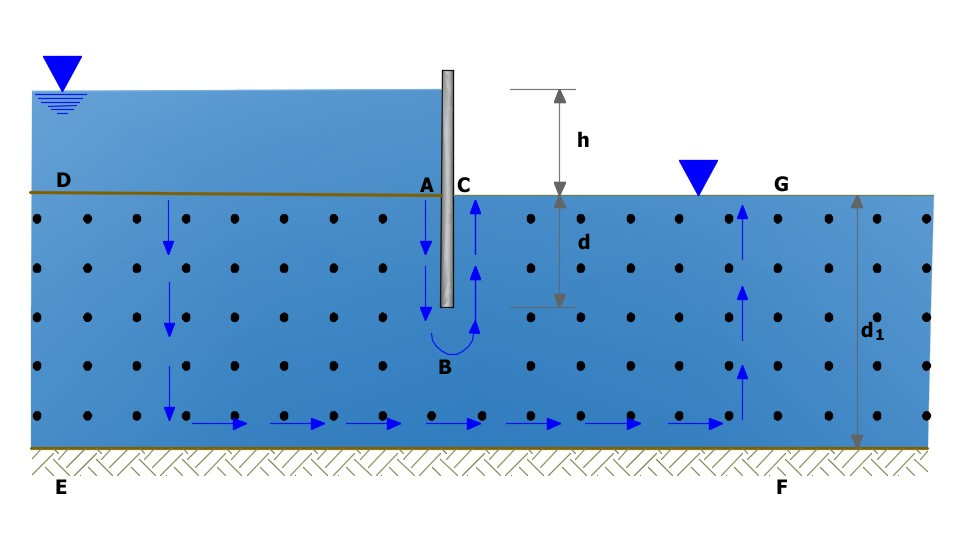
Esquema del flujo de agua
Un caso práctico es el tablestacado de la figura anterior que sostiene un nivel constante h de agua y que está hincado en el terreno a profundidad d en un estrato homogéneo de terreno permeable (arena o grava) de espesor dI, apoyado en un estrato impermeable (roca o arcilla). En este caso se cuenta con un movimiento confinado, ya que las condiciones de contorno de la región son geométricamente definidas. El flujo del agua es causado por la carga hidráulica h; sobre la superficie AD actúa una carga constante y esta superficie constituye el primer confín del potencial de nuestro problema. También en CG la carga es constante y esta superficie constituye el segundo confín. Obviamente, para cumplir con su finalidad, la pantalla debe ser impermeable, por lo que la superficie ABC constituye uno de los confines del flujo, mientras la superficie EF del estrato impermeable forma el otro confín. Evidentemente, si en teoría las características del agua, del suelo y del estrato impermeable en el trasdós y en el intradós de la pantalla se mantienen constantes, se puede considerar que los puntos D, E, F y G sigan al infinito. En la práctica, por lo general se considera que la longitud interesada esté comprendida en 4-5 veces el espesor del estrato. Para determinar la cantidad de agua que se filtra en el terreno se establecen las hipótesis de que el flujo del agua se rija por la ley de Darcy y que el suelo sea homogéneo, isótropo e incompresible:
![]()
Se recuerda que la ley de Darcy es válida para flujo laminar, condición que se verifica con ciertos valores del número de Reynolds, R.
El valor de R, que caracteriza el pasaje de movimiento laminar a turbulento, asume valores diferentes a según del autor.
Taylor (1948) indica como criterio de validez de la ley de Darcy R <= 1.
Otros estudiosos han examinado, especialmente con arcillas, la conexión entre las condiciones de movimiento y el gradiente hidráulico. Tavenas y otros (1983) llegaron a la conclusión de que, en cuanto a las arcillas, la ley de Darcy es válida para gradientes comprendidos entre 0,1 y 50.
Para calcular el caudal de filtración a través del suelo es útil determinar la distribución de la presión de poro construyendo una red de flujo, o sea un sistema de líneas de corriente y líneas equipotenciales que representan el flujo del agua en suelo incompresible. Aceptando la hipótesis de suelo incompresible para los movimientos de filtración planos y en régimen permanente, la ecuación de continuidad se puede escribir así:
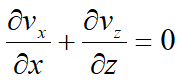
Los dos componentes de la velocidad del líquido, según la ley de Darcy, se pueden expresar así:
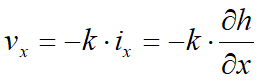
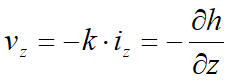
Uniendo estas tres ecuaciones se obtiene:
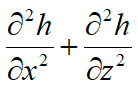
que es la ecuación de Laplace con movimiento permanente en un plano, suponiendo material homogéneo, isótropo e incompresible. Esta ecuación se expresar con dos funciones conjugadas φ y ψ. De hecho, podemos expresar los componentes de velocidad como derivados parciales con respecto a x y z de la función φ = k h por lo tanto:
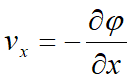

Entonces podemos escribir:
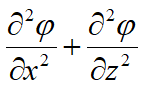
La existencia de la función de potencial de velocidad de un fluido en movimiento φ = k h, implica vorticidad nula y que el movimiento sea irrotacional. Entonces podemos decir que se cuenta con una función de corriente tal que:
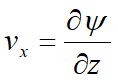
Y por lo tanto:
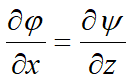
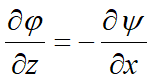
Podemos también decir:
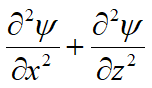
φ y ψ se conocen, respectivamente, como función de potencial y función de corriente. Retomando el caso anterior del agua que se filtra a través del terreno por debajo de una pantalla (figura siguiente), tenemos que dos líneas equipotenciales son las superficies del terreno del trasdós y del intradós de la misma y además la superficie del estrato impermeable es una línea de corriente o de flujo. Resolviendo la ecuación de Laplace de acuerdo con estas condiciones límite, podemos construir la red de flujo. Cada franja comprendida entre dos líneas de flujo adyacentes es un canal de flujo y cada parte del canal de flujo comprendida entre dos líneas equipotenciales es un campo. Por lo tanto es conveniente construir las líneas equipotenciales en manera tal que desnivel piezométrico entre dos líneas sucesivas sea constante y las líneas de flujo en manera tal que cada canal de flujo tenga un caudal constante. Si h es la carga hidráulica total y Na es el número de desniveles piezométricos identificados, la diferencia de carga hidráulica entre dos líneas equipotenciales sucesivas es:
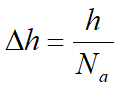
En un punto z como se indica en la figura siguiente, la presión vale:
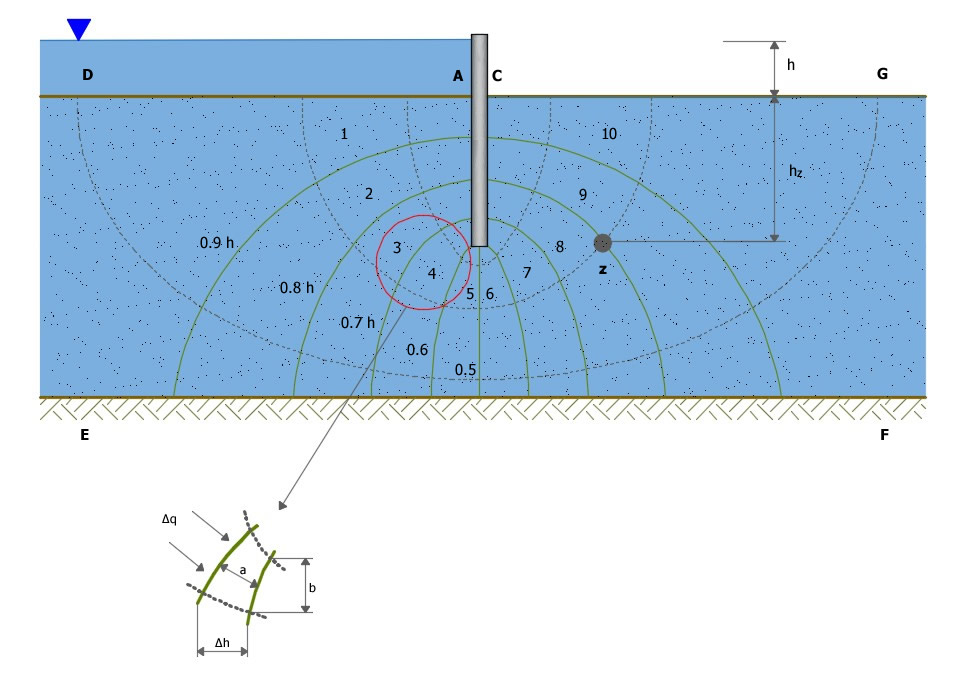
Esquema de la red de flujo
siendo n el número de desniveles piezométricos atravesados para llegar a z. En el ejemplo anterior tenemos:
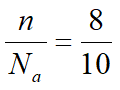
Si no hubiese flujo de agua, o sea si la superficie del intradós fuese impermeable, la presión hidrostática en este punto sería:
![]()
Dado el agua se mueve, tenemos un pérdida de carga que, según la red de filtración dibujada en el punto z, es igual a 8/10h. La sobrepresión del agua en el punto z es dada por:
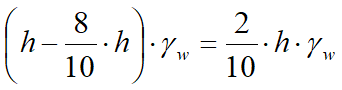
Para conocer el caudal de filtración consideramos un campo, o sea un área comprendida entre dos líneas de flujo y dos líneas equipotenciales. La longitud del lado en la dirección de las líneas de flujo es a y por lo tanto el gradiente hidráulico en un campo es:
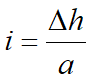
y la velocidad:
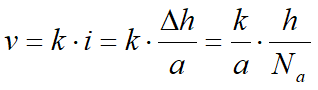
Supongamos que el otro lado del campo sea de longitud b, entonces el caudal a través del campo por unidad de longitud de pantalla sería:
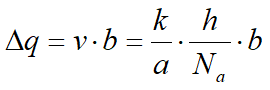
para cada tubo de flujo; si se indica b = a, o sea si los elementos de la red de filtración son cuadrados, se obtiene:
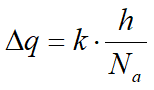
Si Nb es el número total de canales de flujo, el caudal total por unidad de longitud de pantalla es:
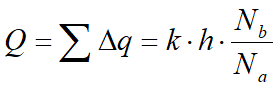
De este modo, una vez construida la red de flujo, se puede calcular fácilmente el caudal. La red de filtración generalmente se construye en laboratorio con métodos experimentales, con modelos analógicos o gráficamente por prueba y error. En situaciones más complejas del subsuelo, con sucesión de estratos y anisotropía de la permeabilidad, se puede obtener la red de filtración mediante métodos numéricos (FEM, BEM, método de las diferencias finitas).
© Geostru