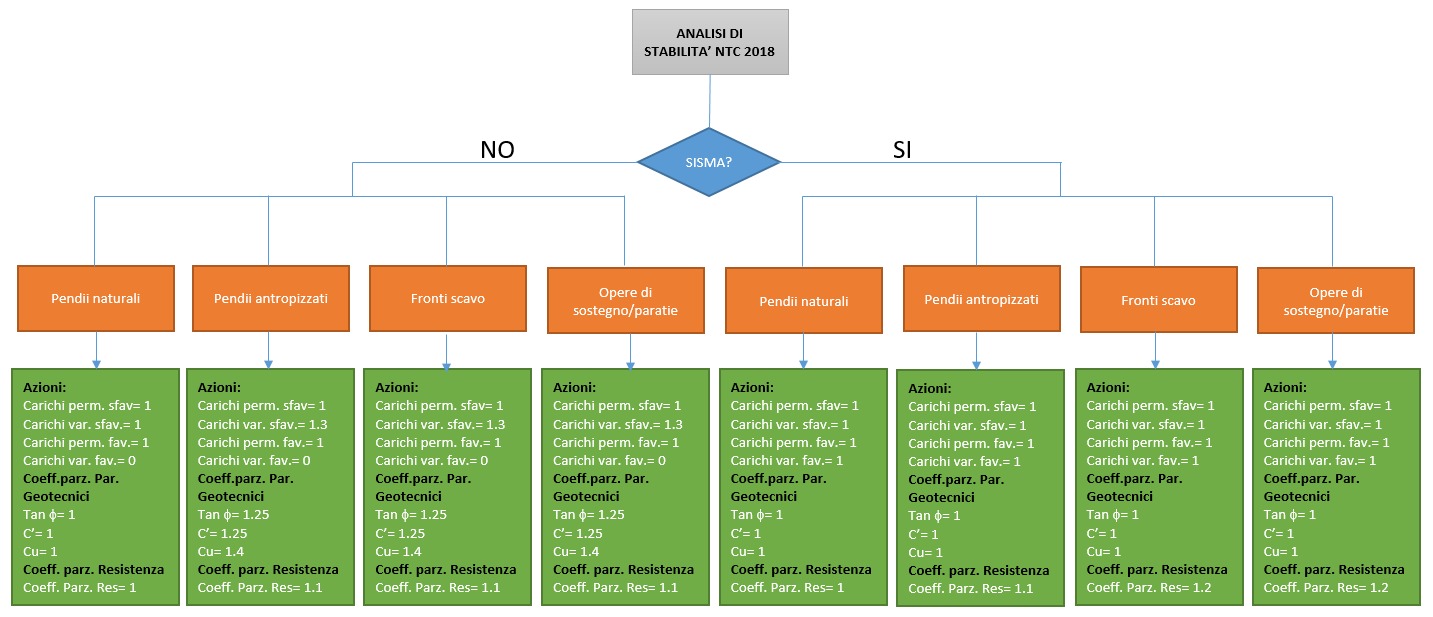
Problema geotecnico

Condizioni statiche

Condizioni sismiche

Si introducono le azioni sismiche/forze d’inerzia (*)

Pendii naturali

Utilizzare i parametri caratteristici sia per le azioni che per i parametri geotecnici non bisogna considerare la riduzione sulla resistenza del sistema

Parametri caratteristici come per le condizioni statiche.

Fronti di scavo-Rilevati

Combinazione A2+M2+R2:

γA2, γM2 (cfr. tab. 2.6.I)(cfr. tab. 6.2.I e tab. 6.2.II)

γR2=1.1

Combinazione A2+M2+R2 con:

γA2=1, γM2=1, γR2=1.2

βs=0.38 per SLV

βs=0.47 per SLD

Pendii antropizzati

Combinazione A2+M2+R2:

γA2, γM2 (cfr. tab. 2.6.I)(cfr. tab. 6.2.I e tab. 6.2.II)

γR2=1.1

Combinazione A2+M2+R2 con:

γA2=1, γM2=1, γR2=1.1

Fondazioni superficiali

Combinazione A1+M1+R3 (STR+GEO):

γA1(cfr. tab. 2.6.I),

γM1=1

γR3=2.3 Carico limite

γR3=1.1 Scorrimento

Combinazione A1+M1+R3 (STR+GEO)

γA1= γM1 =1

γR3=1.8 Carico limite, se si considera l’azione inerziale altrimenti γR3=2.3

Kh e βs come pendii naturali

Fondazioni profonde

Combinazione A1+M1+R3 (STR+GEO)

γA1, γM1 (cfr. tab. 2.6.I)

γR3 (cfr. tab. 6.4.II)

γR3 = 1.3 per carichi trasversali

Combinazione A1+M1+R3 (STR+GEO)

γA1= γM1 =1

γR3 (cfr. tab. 6.4.II)

γR3 = 1.3 per carichi trasversali

Fondazioni Miste

Combinazione A1+M1+R3

Carico limite assiale

γA1 (cfr. tab. 2.6.I)

γM1=1, γR3=2.3

Carico limite trasversale

γA1 (cfr. tab. 2.6.I)

γM1=1, γR3=1.3

Verifica di stabilità globale:

A2+M2+R2

γA2, γM2 (cfr. tab. 2.6.I)

γR2=1.1

Combinazione A1+M1+R3

Carico limite assiale

γA1= γM1=1, γR3=2.3

Carico limite trasversale

γA1= γM1=1, γR3=1.3

Verifica di stabilità globale:

A2+M2+R2

γA2= γM2 =1

γR2=1.1

Kh e βs come pendii naturali

(****)

Opere di sostegno

Combinazione A1+M1+R3 (STR+GEO)

γA1 (cfr. tab. 2.6.I), γM1=1

γR3 (cfr. tab. 6.5.I)

Verifica di stabilità globale:

A2+M2+R2

γA2, γM2 (cfr. tab. 2.6.I)

γR2=1.1

Combinazione A1+M1+R3 (STR+GEO)

γA1= γM1 =1

βs=0.38 per SLV

βs=0.47 per SLD

γR3 (cfr. tab. 7.11.III)

Verifica a ribaltamento:

γA1= γM1 =1

βs incrementato del 50%

γR3 (cfr. tab. 7.11.III)

Verifica di stabilità globale:

A2+M2+R2

γA2= γM2 =1

γR2=1.2

Paratie

•Combinazione 1 (STR): (A1+M1+R1)

•Combinazione 2 (GEO): (A2+M2+R1)

γA1, γM1,γA2, γM2 (cfr. tab. 2.6.I)

γR1=1

Verifica di stabilità globale:

A2+M2+R2

γA2, γM2 (cfr. tab. 2.6.I)

γR2=1.1

Unica combinazione con:

γA= γM =γR=1

Si introduce ah (componente verticale dell’accelerazione) per la stima delle forze d’inerzia.

ah = kh∙g = α∙β∙amax  (**)

Verifica di stabilità globale:

A2+M2+R2

γA2= γM2 =1

γR2=1.2

Tiranti di ancoraggio

Combinazione A1+M1+R3 (GEO+STR)

Verifica a sfilamento fondazione (bulbo-terreno).

Verifica a rottura dell’armatura

γA1, γM1 (cfr. tab. 2.6.I)

γR3=1.1 tiranti temporanei

γR3=1.2 tiranti permanenti

(***)

Combinazione A1+M1+R3 (STR+GEO)

γA1= γM1 =1

ah = kh∙g = β∙amax  (*****)

γR3=1.1 tiranti temporanei

γR3=1.2 tiranti permanenti

Va incrementata la lunghezza libera del tirante:

Le=Ls=(1+1.5 ∙ amax/g)

Ls= lunghezza libera in condizioni statiche

OSSERVAZIONI

(*)

Fh=kh∙W (componete orizz.)

Fv=kv ∙W (componente vert.)

kh=βs∙(amax/g)

kv=0.5∙ kh

(**)

Il valore del coefficiente β può essere ricavato dal diagramma di Fig. 7.11.3, in funzione del massimo spostamento permanente us che l’opera può tollerare, verificando l’effettivo sviluppo di meccanismi duttili nel sistema. In assenza di tale verifica, il coefficiente β vale 1.Il valore di α è funzione del tipo di suolo e dell’altezza totale della paratia.

(***)

Per i tiranti delle paratie, l’azione di progetto sull’ancoraggio si ottiene amplificando, mediante i coefficienti A1, l’azione caratteristica calcolata mediante un’analisi che porti in conto, anche in maniera semplificata, l’interazione fra paratia e terreno, operando su configurazioni che rispettino l’equilibrio e la compatibilità con il criterio di resistenza, e nella quale tutti i coefficienti parziali sulle azioni e sui parametri di resistenza siano unitari.

(****)

Se la capacità portante della fondazione diretta è sufficiente ai pali può essere affidata la sola funzione di controllo e regolazione del cedimento.

Se la capacità portante della fondazione diretta è invece insufficiente, è possibile tenere conto del contributo dei pali nell'analisi dei seguenti stati limite ultimi:

▪collasso della fondazione mista nei riguardi dei carichi assiali;

▪collasso per carico limite della fondazione mista nei riguardi dei carichi trasversali.

Per la resistenza della fondazione mista nei confronti del collasso per carico limite orizzontale, occorre in primo luogo eseguire un'analisi di interazione pali-struttura di collegamento-terreno, al fine di pervenire alle aliquote di ripartizione fra platea e pali sia dei carichi assiali sia dei carichi trasversali.

A questo punto la verifica viene effettuata per le due componenti della fondazione mista, secondo le prescrizioni di cui ai §§ 7.11.5.3.1 e 7.11.5.3.2. Se invece l'interazione fra la struttura di collegamento e i pali viene giudicata non significativa, o si omette la relativa analisi, il carico orizzontale deve essere affidato integralmente ai pali, e le verifiche della palificata nei confronti dei carichi trasversali vanno effettuate con le prescrizioni di cui al § 7.11.5.3.2.

(vedi §7.11.5.3.2 Fondazioni su pali)

(*****)

Se non viene rispettato il principio di gerarchia delle resistenze occorre considerare β vale 1.