Probabilitatea
Teoria probabilităților este studiul matematic al probabilităților.
Matematicienii se referă la probabilități ca fiind numere din intervalul 0-1, atribuite unor "evenimente" a căror apariție este aleatorie.
Probabilitatea este un număr asociat unui eveniment (rezultat în urma observării unui experiment) care poate să se producă sau nu.
Probabilitatea clasică a priori
Dacă N este numărul total de cazuri din spațiul de eșantionare al unei variabile aleatoare și n este numărul de cazuri favorabile pentru care se realizează evenimentul A, probabilitatea a priori a lui A este dată de:
![]()
Probabilitatea a priori poate lua o valoare între 0 și 1. O probabilitate egală cu 0 indică faptul că evenimentul este imposibil, iar o probabilitate egală cu 1 indică faptul că evenimentul este sigur.
Probabilitatea cea mai frecventă
Dacă m este numărul de încercări în care a avut loc evenimentul A la un total de M încercări, probabilitatea lui A este dată de:
![]()
Limita care apare în această definiție nu trebuie înțeleasă în sens matematic, ci în sens experimental: adevărata valoare a probabilității se găsește numai prin efectuarea unui număr infinit de încercări.
Indicatori ai unei distribuții statistice
Descrierea datelor dintr-un eșantion statistic se face prin determinarea distribuției frecvențelor relative, care conține implicit toate informațiile care pot fi extrase din eșantion.
Indicatorii sunt parametri care descriu cantitativ aspectele generale ale distribuției statistice.
•În teoria probabilităților, probabilitatea sau funcția de distribuție a unei variabile aleatoare discrete x este o funcție a unei variabile reale care atribuie fiecărei valori posibile a lui x probabilitatea evenimentului respectiv.
•Valoarea așteptată m (numită și medie sau speranță) a unei variabile reale aleatoare x este un număr care formalizează ideea euristică de valoare medie a unui fenomen aleator și se definește astfel:

•Varianța unei variabile aleatoare x este un număr Var(x), care oferă o măsură a cât de diferite sunt valorile luate de variabilă, adică cât de mult se abat de la media m. Varianța lui x este definită ca fiind valoarea așteptată a pătratului variabilei aleatoare centrate. În statistică este adesea preferată rădăcina pătrată a varianței lui x, abaterea standard indicată prin litera σ. Din acest motiv, varianța este indicată cu σ2. În statistică, se utilizează de obicei doi estimatori pentru varianța unui eșantion de cardinalitate n:
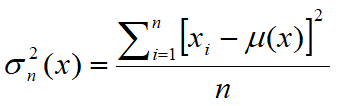 și
și 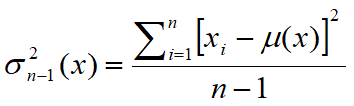
Estimatorul sn-1 are o valoare așteptată egală cu varianța sa, în schimb, estimatorul sn are o valoare diferită de varianța așteptată. O justificare a termenului n-1 este dată de necesitatea de a estima și media. Dacă media μ este cunoscută, estimatorul sn devine corect.
•Pornind de la abaterea standard, se definește, de asemenea, coeficientul de variație sau abaterea standard relativă ca fiind raportul dintre abaterea standard și media aritmetică a valorilor:
![]()
Acest nou parametru (adesea folosit ca procent) este utilizat pentru a face comparații între diferite tipuri de dispersie a datelor, indiferent de valorile lor absolute.
Modul în care este distribuită probabilitatea unei variabile aleatoare depinde de mulți factori și, întrucât există o infinitate de grafice posibile ale funcțiilor, putem avea modalități infinite pentru diferite distribuții de probabilitate.
Cele mai semnificative distribuții de probabilitate sunt:
1)Distribuția normală
2)Distribuția logaritmică normală
3)Distribuția t a lui Student
Distribuția normală
Variabila aleatoare Normală (numită și variabilă aleatoare Gaussiană sau curbă Gaussiană) este o variabilă aleatoare continuă cu doi parametri, indicată convențional cu:
![]()
Este una dintre cele mai importante variabile aleatoare, în special continue, deoarece este baza de pornire pentru celelalte variabile aleatoare (Chi pătrat, Student t, F Snedecor etc.). Variabila aleatoare Gaussiană se caracterizează prin următoarea funcție de densitate de probabilitate, la care se referă adesea termenul de curbă Gaussiană sau Gaussiană:

unde x este mărimea a cărei probabilitate trebuie să o calculăm
![]()
Și unde μ și σ reprezintă media populației și abaterea standard. Ecuația funcției de densitate este construită astfel încât aria de sub curbă să reprezinte probabilitatea. Prin urmare, aria totală este egală cu 1.
Una dintre cele mai vizibile caracteristici ale distribuției normale este forma și simetria perfectă. Observați că, dacă pliați imaginea distribuției normale exact la mijloc, veți avea două jumătăți egale, fiecare fiind o imagine în oglindă a celeilalte. Acest lucru înseamnă, de asemenea, că o jumătate din observațiile din date se încadrează de fiecare parte a mijlocului distribuției.
Punctul de mijloc al distribuției normale este punctul care are frecvența maximă. Adică, este numărul sau categoria de răspuns cu cele mai multe observații pentru acea variabilă. Punctul de mijloc al distribuției normale este, de asemenea, punctul în care se află trei măsuri: media, mediana și modul. Într-o distribuție normală perfectă, aceste trei măsuri sunt toate trei același număr.
Recurgând la standardizarea (statistică) variabilei aleatoare, adică la transformarea astfel încât:
![]()
unde variabila rezultată
![]()
are, de asemenea, distribuție normală cu parametrii μ = 0 și σ = 1, curba lui Gauss poate fi scrisă sub forma:
![]()
Valoarea caracteristică poate fi estimată cu ajutorul expresiei:
![]()
Cu o probabilitate de 5%, Z (din tabel) este egal cu -1,645, astfel încât expresia de mai sus poate fi rescrisă sub forma:
![]()
Împărțind ambele părți cu media μ, relația devine:
![]()
Distribuția logaritmică normală
O variabilă aleatorie x are o distribuție log normală cu parametrii μ de exemplu, dacă ln(x) este distribuită normal cu media μ și abaterea standard s.
În mod echivalent:
![]()
și
![]()
unde y este distribuită normal cu media μ și abaterea standard s.
Parametrul μ poate fi orice real, în timp ce s trebuie să fie pozitiv.
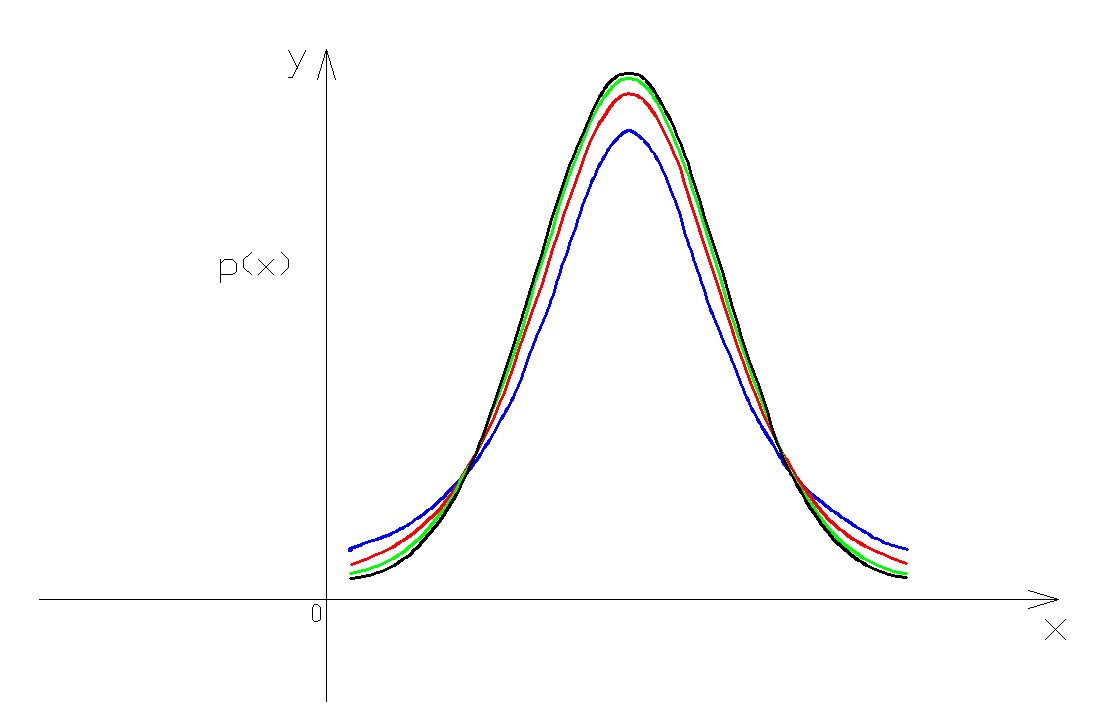
Curba de distribuție a probabilității are următoarea formă:
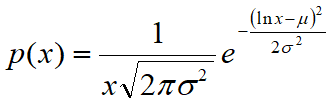
Din cauza asimetriei curbei, valorile mediei, modului și medianei nu coincid, spre deosebire de ceea ce se întâmplă în schimb în distribuția normală. Punctul maxim al curbei este, de fapt, deplasat spre stânga față de valoarea medie.

Distribuția t a lui Student
Distribuția t a lui Student ia în considerare relația dintre medie și varianță în eșantioane mici, extrase dintr-o populație distribuită normal, folosind varianța eșantionului.
Având în vedere o populație distribuită normal, se extrage un eșantion aleatoriu de n observații și se calculează variabila aleatoare t, definită de următoarea ecuație:
![]()
Unde s este varianța eșantionului.
t urmează o lege t a lui Student cu n-1 grade de libertate. Cantitatea de la numărător se numește eroarea standard a eșantionului.
Forma distribuției depinde de gradele de libertate, adică de mărimea eșantionului. Pentru n mare (>30) t tinde spre o normală.
Regula celor trei sigme
Într-o distribuție normală, 99,73% dintre măsurători se încadrează la o distanță față de valoarea medie de trei ori deviația standard, adică există o probabilitate de 99,73% ca o măsură extrasă aleatoriu din populație să se situeze la o distanță de ± 3s față de media m.
Odată cunoscută, cea mai mare valoare măsurată în populație dată de:
![]()
iar cea mai mică:
![]()
abaterea standard a populației poate fi calculată astfel:
![]()
Teorema lui Bayes
Teorema lui Bayes, propusă de Thomas Bayes, derivă din două teoreme fundamentale ale probabilității: teorema probabilității și teorema probabilității absolute. Ea este adesea utilizată pentru a calcula probabilitățile posterioare date de observații.
Această teoremă poate fi exprimată sub forma:
![]()
Unde:
P(A) a priori, este gradul inițial de credință în A (probabilitatea ca evenimentul A să se producă)
P(A\B) el este posterior, este gradul de credință după ce s-a ținut cont de B (probabilitatea ca evenimentul A să se producă dacă se produce evenimentul B)
P(B\A) este probabilitatea ca evenimentul B să se producă dacă se produce evenimentul A
P(B\A') probabilitatea ca evenimentul B să se producă dacă nu se produce în cazul A=1-P(B\A)
P(A') probabilitatea ca acesta să nu se producă, evenimentul A=1-P(A).
|
©GeoStru