Dato un palo a comportamento non dissipativo in c.a. immerso in argilla, si vuole calcolare il carico limite trasversale da assegnare nell'archivio tipologie pali (§2.2.21).
Come illustrato nel §4.7 il calcolo della resistenza trasversale non può essere eseguito con la teoria di Broms(1964) in quanto essa prevede la formazione di cerniere plastiche dotate di grande duttilità rotazionale incompatibili, pertanto, con il comportamento 'sostanzialmente elastico' che il programma prevede per tutte le strutture di fondazione (pali compresi).
Quindi, a meno di compiere un separato calcolo di duttilità delle armature longitudinali e staffe, può utilizzarsi la modalità di calcolo con terreno non lineare con curve p-y selezionabile nella finestra di Dati Generali. Questa modalità prevede che il comportamento del palo rimanga in elasticità lineare anche se il terreno laterale e di base si comporta in modo non lineare.
TERRENO COERENTE
A scopo di confronto si fa riferimento allo stesso palo descritto nel § 4.7 con rotazione della testa impedita che, grazie alla ipotizzata rotazione plastica delle cerniere (vedi figura seguente), conduce ad un carico di collasso trasversale del palo pari a 383.92 kN.
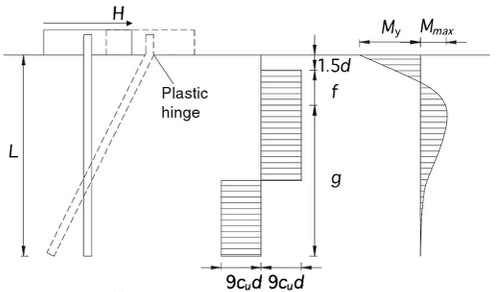
In questo modello con palo a comportamento 'sostanzialmente elastico' il carico di collasso H , invece, corrisponde al carico che produce il momento di rottura nella sezione di massima sollecitazione (in questo caso all'attacco del palo con la testata). Cioè fino a quando la sezione più sollecitata del palo non va a rottura il palo non passa mai in fase plastica in quanto non viene mai superato, in ogni sua sezione, il momento di rottura. In modalità non dissipativa ('sostanzialmente elastica') la rottura a presso-flessione della sezione del palo può avvenire per eccesso di deformazione del calcestruzzo (e>0.002) o dell'acciaio (e>fy/Es) ma sempre in presenza della massima percentuale di armatura longitudinale di normativa (4% Ac). H. Per stimare il carico orizzontale Hlim di collasso si tratta quindi di incrementare il carico nodale H orizzontale fino a quando non si rompe la sezione più sollecitata del palo (cioè fino a quando il palo risulta per l'ultimo tentativo ancora verificato).
Per il calcolo con il suddetto carico di collasso occorre aprire un apposito nuovo calcolo (Esempio_3.F3F) e selezionare come modellazione dei pali quella Non lineare (curve p-y, t-z). Se, come di consueto, le massime forze orizzontali corrispondono alle sollecitazioni sismiche, la prima ed unica combinazione nodale assegnata va indicata come sismica (cioè come non dissipativa):
La sezione del palo va definita nell'Archivio sezioni travi/pali: qui si fissa il diametro del palo (60 cm), il copriferro (cf = 5 cm), il tipo di calcestruzzo (C25/30), il tipo di acciaio (B450C).
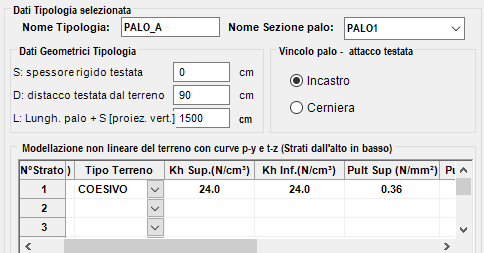
Il terreno viene modellato (secondo lo schema di Broms sopra illustrato) nell'Archivio tipologie pali in modalità non lineare assegnando la lunghezza del palo L = 1500 cm ed il primo tratto del fusto pari a 1.5 d = 90 cm come distacco D testata-terreno. Il diagramma tensioni-deformazioni trasversale di tipo iperbolico con pressione massima costante pari a Pult = 9 · Cu = 9 ·0.04= 0.36 N/mm². Il valore di Kh viene dedotto dalle correlazioni: Kh = 1.2 · Es /d in cui Es = 300 · Cu = 300 · 0.04 = 12 N/mm² =1200 N/cm². Quindi Kh = 1.2 · 1200/60 = 24.0 N/cm³.
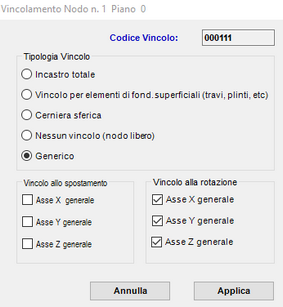
Nella scheda di Input Vincoli esterni va imposto (in corrispondenza del nodo n. 1 in cui è stato posto il palo) il vincolo alla rotazione della testa del palo (pattino) in questo modo:
Sempre nella scheda id Input e dopo aver selezionato l'unica combinazione nodale di carico assegnata, vanno assegnate le sollecitazioni nodali pari a FX kN come forza orizzontale (da incrementare fino a rottura del palo) e FZ = -460 kN = carico verticale minima agente sul nodo nelle combinazioni sismiche.
Dopo qualche tentativo (modificando solo FX) si ottengone che il massimo valore di FX che verifica il palo risultati pari a Fx = 330 kN ( con 34F20 (pari a circa il 4% di Ac). Ottenuto il carico di collasso si ricava la resistenza traversale caratteristica Hk= H/1.7 ed infine la resistenza trasversale di progetto Hd= Hk/1.3 da inserire nell'Archivio Tipologie Pali.
Si noti nel §4.7 si era ottenuto il carico di collasso H = 384 kN (applicando la teoria di Broms) con appena 16 F16 (pari a 1.1%) grazie all'ipotesi di cerniera plastica ad alta duttilità.
Anche se comporta un maggiore impiego di armature il metodo qui illustrato di calcolo del carico H di collasso ne consente la valutazione anche nel caso di terreno stratificato con sensibili escursioni di rigidezza (cosa non possibile con la teoria di Broms originale).
TERRENO INCOERENTE
Nell'ESEMPIO3_BIS si è modellato il terreno incoerente omogeneo con la schematizzazione prevista nella teoria di Broms ed illustrata dalla figura seguente:
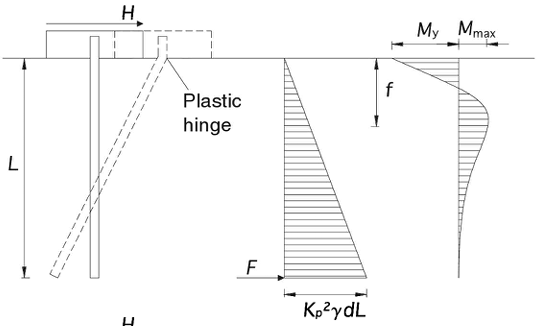
Il valore Kp della pressione passiva del terreno si ottiene a partire dal valore dell'angolo di attrito F' assunto qui pari a 32°. Pertanto Kp=tang²(p/4+F'/2) = 0.091.
Posti g =0.00018 N/mm²; d= 600 mm e L = 15000 mm si ha Pult = 13.41 N/mm²
Per Kh si assume un valore costante di Kh = 24 N/cm³.
Con la stessa metodologia prima esposta si risolve per successivi tentativi la struttura applicando una forza orizzontale FX via via crescente fino a ottenere la non verifica del palo (per rottura della sezione più sollecitata del palo). Il massimo carico per cui il palo risulta ancora verificato è FX = 400 kN. Quindi il carico di collasso risulta Hlim = 400 kN. Quindi Kk = 400/1.7 = 235,29 kN. Hd =235.29/1.3 = 181.00 kN. Lo stesso calcolo svolto con la teoria di Broms (§4.7) e armatura dell'1%, conduce, invece, ad un carico di collasso Hlim = 572 kN.
.
Geostru Software ©