PREMESSA METODOLOGICA SUL CALCOLO DELLE PALIFICATE
Una prima importante distinzione da fare è quella tra pali isolati e pali in gruppo. Possono considerarsi isolati quei pali disposti in modo che la loro distanza reciproca superi 6÷8 volte il loro diametro (ad esempio pali che portano singolarmente i pilastri e siano collegati da un graticcio di travi o da una platea). I pali che invece sono più vicini della suddetta distanza (di estinzione) e che siano tra loro collegati da un unica testata vanno considerati come pali in gruppo (ad esempio ogni plinto su pali realizza un gruppo; come pure una platea su pali ravvicinati).
Per evitare eccessive interazioni e quindi eccessivi cedimenti assiali i pali non devono mai essere a distanza reciproca minore di 3 volte il loro diametro.
Per i pali isolati la resistenza di progetto (GEO) assiale e trasversale va calcolata con riferimento ad ognuno di essi, dividendo le resistenze ultima per i fattori di correlazione (§ 6.4.3.1.1, § 6.4.3.1.2). Ottenute così le resistenze caratteristiche queste vanno a loro volta divise per i coefficienti parziali R3 per ottenere le resistenze di progetto con cui verificare singolarmente i pali. Anche i cedimenti dei pali vanno verificati palo per palo (cedimenti e rotazioni differenziali devono essere valutati dal progettista sulla scorta dei cedimenti assoluti forniti dal programma).
Per i pali in gruppo le NTC fanno una precisa distinzione tra il calcolo di resistenza per gli SLU e quello degli SLE, quest'ultimo orientato prevalentemente al calcolo degli spostamenti e distorsioni. Mentre per il primo tipo di calcolo (SLU) viene richiesto di tener conto delle possibili riduzioni di resistenza per effetto di gruppo, per il secondo oltre all'effetto di gruppo si chiede di tenere opportunamente conto, nel calcolo dei cedimenti, degli effetti di interazione tra i pali. Mettere in conto l'effetto di gruppo (sia nelle verifiche SLU che in quelle SLE) consiste in pratica nel valutare (caso per caso) due fattori di efficienza (uno per forze assiali, l'altro per forze trasversali) mediante i quali ridurre la somma delle resistenze complessive dei pali. Mettere in conto, nelle verifiche SLE, gli effetti di interazione (essenzialmente quelli assiali per carichi verticali) significa invece valutare con maggiore attenzione i maggiori cedimenti e distorsioni che tali effetti vanno a produrre sia nella struttura di fondazione che nella sovrastruttura. Poichè in questo programma è stata prevista una valutazione specifica dell'interazione assiale tra i pali basata sul metodo dei coeff. di influenza si consiglia di effettuare due distinti calcoli della stessa struttura di fondazione su pali:
1) Un primo calcolo contenente le sole combinazioni SLU/SLV con la definizione dei fattori di efficienza per effetti di gruppo senza mettere in conto l'interazione assiale tra i pali (tranne nel caso di fondazioni miste di cui al § 3.4 di questo manuale).
2) Un secondo calcolo contenente le sole combinazioni SLE in cui oltre ad i fattori di efficienza per effetti di gruppo si consideri l'interazione assiale tra i pali. Oltre alle SLE vanno definite SLU fittizie con gli stessi sforzi applicati onde progettare le armature dei pali e delle strutture di collegamento dei pali per le sollecitazioni SLE (il programma non progetta le armature con le sole SLE) .
Le armature finali del progetto risulteranno dall'inviluppo di quelle verificate in entrambi i calcoli. Per una migliore stima dei cedimenti nelle verifiche SLE per carichi verticali, si consiglia di utilizzare l'opzione del calcolo non lineare del comportamento del palo per azioni assiali (metodo di chin)( vedasi Esempio 7).
Altra importante norma introdotta dalle NTC 2018 è contenuta nel § 6.4.3.1.1.1:
"Per una palificata, la verifica della condizione [6.2.1] dovrà essere fatta in base alla resistenza caratteristica che risulta dalla somma delle resistenze caratteristiche dei pali che la costituiscono. Sarà comunque necessario valutare possibili riduzioni della resistenza disponibile per effetto di gruppo, tenendo conto della tipologia dei pali, della natura dei terreni interessati e della configurazione geometrica della palificata".
Quindi per pali in gruppo distanti tra loro meno di 6 volte il diametro non andrebbe verificata la resistenza assiale di progetto di ogni palo bensì quella caratteristica somma delle resistenze caratteristiche di tutti i pali del gruppo. Ad avviso di chi scrive l'applicazione di questa norma dovrebbe essere fatta prevedendo un calcolo dei pali assialmente non lineare (la resistenza non deve poter superare quella limite di ogni palo). Di conseguenza (prudenzialmente) questo programma in presenza di pali in gruppo (plinti su pali predefiniti e pali tra loro a distanza minore di 6 volte il loro diametro ed indicati nei Dati Generali con il fattore di efficienza Ev<1), continua sì ad effettuare la verifica di resistenza assiale di singolo ogni palo del gruppo, ma lo fa confrontando la forza assiale di combinazione agente sul palo con la resistenza caratteristica e non con la resistenza di progetto (come precedentemente previsto). Per operare questa innovativa verifica l'utente deve assegnare (in questo archivio tipologie pali) al posto della resistenza assiale di progetto quella caratteristica. Naturalmente il programma esegue comunque la verifica di gruppo assiale e trasversale in base ai fattori di efficienza assegnati in input.
Sono previsti 3 tipologie dei pali (e corrispondenti archivi) a seconda della modellazione del terreno (il palo resta sempre a comportamento lineare):
1) Pali in terreno stratificato alla Winkler (lineare)
2) Pal in terreno stratificato non lineare (curve p-y, t-z)
3) Pali in terreno solo assialmente non lineare (modello iperbolico di Chin)
Per ogni calcolo si può utilizzare solo una delle tre schematizzazioni e la relativa scelta va fatta nella finestra dei Dati Generali (§ 2.2.2). Se, come sopra consigliato, si vuole svolgere separatamente e linermante il calcolo SLU/SLV rispetto a quello non lineare SLE, basta fare la copia (Salva file con nome) del primo calcolo e variare le impostazioni nei Dati Generali e le combinazioni di carico.
Per tutte le tipologie gli archivi vanno comunque assegnati i cedimenti e gli spostamenti trasversali orizzontali limite dei pali sia in riferimento agli SLU che agli SLE (§ 6.4.3.2 NTC). Questi valori limite vanno decisi in funzione dei requisiti prestazionali della struttura in elevazione. Particolare attenzione va rivolta ai cedimenti verticali in esercizio quando vengono impiegati pali di grande diametro poichè la maggiore aliquota di portanza alla punta può essere raggiunta solo a prezzo di cedimenti verticali molto elevati (cap.13 Viggiani [7]). La valutazione sull'accettabilità dei cedimenti differenziali e delle distorsioni rotazionali resta a carico dell'utente che deve effettuare tale valutazione sulla scorta dei risultati prodotti dal programma.
Nel caso di pali in gruppo i cedimenti verticali dei pali calcolati dal programma nel caso di interazione elastica col terreno sono approssimati in quanto calcolati elasticamente e senza tener conto della non linearità dei cedimenti assiali dei pali. Se si effettuano prove di carico su pali pilota (meglio se strumentati) o anche su pali di prova, si può ottenere una migliore approssimazione nei risultati utilizzando il metodo della curva carichi-cedimenti iperbolica di Chin (tipologia 3). Più difficile il miglioramento dell'approssimazione utilizzando le curve di trasferimento (p-y)(t-z) (tipologia 2 più adatta per la valutazione degli spostamenti orizzontali SLV).
Di seguito verranno illustrati i tre tipi di archivio.
TIPOLOGIA PALI ALLA WINKLER con terreno elastico lineare
Il terreno può essere stratificato con caratteristiche differenti da strato a strato. Per ogni strato è possibile definire una costante di winkler trasversale varibile linearmente da un valore superiore (all'estremo superiore dello strato) ed un valore inferiore (all'estremo inferiore dello strato). Per ogni strato il tratto di palo in esso ricadente viene discretizzata in conci nei cui estremi viene condensata la rigidezza del terreno (come sopra assegnata) a mezzo di molle a comportamento elastico lineare (cfr § 1.10).
La rigidezza elastica assiale del palo viene valutata con la formule di Randolph-Wroth-Fleming descritta nel § 3.3.
Questo modello prevede il calcolo dell'interazione assiale tra i pali in gruppo mediante l'impiego dei coeff. di influenza (da utilizzare solo per pali in gruppo e nel caso di fondazioni miste (§ 3.4). L'ipotesi di linearità delle rigidezze assiali rende i risultati dell'interazione palo-terreno meno affidabili di quelli in cui la rigidezza assiale è di tipo non lineare (si veda veda la tipologia basata sul modello iperbolico di Chin(1970)), in quanto i risultati dipendono fortemente dalla rigidezza costante assegnata (la non linearità modifica molto detta l'interazione).
Per ogni tipo di palo identificato con un qualsiasi nome vanno assegnati i seguenti ulteriori dati:
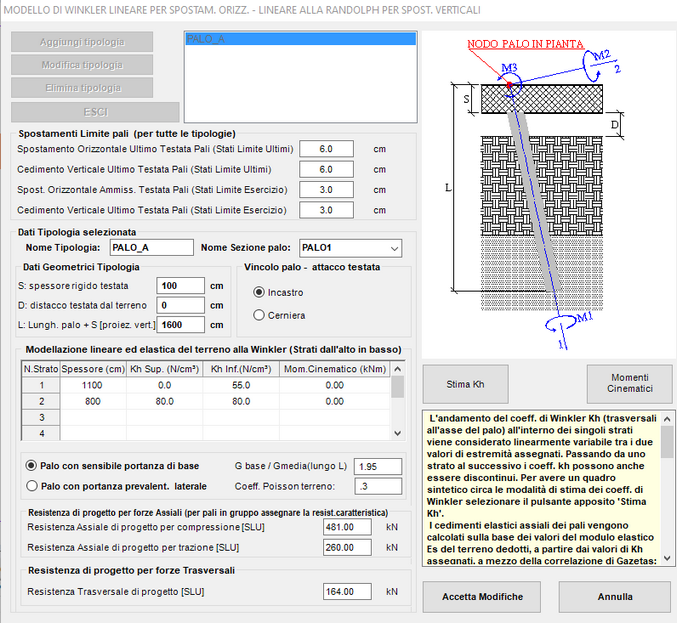
Nome Sezione trasversale
Va selezionata una delle sezioni di palo presenti nell'Archivio sezioni travi-pali (§ 2.2.17).
S, D, L
•S è lo spessore dell'eventuale platea o plinto in cui è incastrato o incernierato il palo. Se S > 0 viene generato un concio rigido che collega il nodo di riferimento del palo, posto sull'estradosso della testata, al punto di inizio del tratto flessibile del palo. E' importante indicare correttamente questo spessore ai fini del corretto calcolo della fondazione.
•D è l'eventuale distacco del terreno resistente dall'intradosso della testata; può essere assegnato anche per tener conto dello spessore dello strato superficiale del terreno se di resistenza inconsistente.
•L è la somma della lunghezza del palo con lo spessore S della testata misurata in proiezione verticale (nel caso di pali inclinati)
Dati Strati terreno (dall'alto verso il basso)
Spessore Strato (cm): per ogni strato va indicato il suo spessore
Kh Sup (N/mm²): è il valore del coefficiente di sottofondo orizzontale da assegnare alla quota superiore del singolo strato; per la sua stima possono essere utili le indicazioni (per calcolo lineare) contenute nella finestra che si apre tramite il pulsante "Stima Kh"
Kh Inf (N/mm²): è il valore del coefficiente di sottofondo orizzontale da assegnare alla quota inferiore del singolo strato; per la sua stima possono essere utili le indicazioni (per calcolo lineare) contenute nella finestra che si apre tramite il pulsante "Stima Kh"
Mom. Cinematico (kNm): nel caso in cui due strati contigui di terreno presentino al contatto un elevato contrasto di rigidezza (rapporto >5÷6) il punto 7.11.5.3.2 delle NTC prescrive la valutazione dei momenti per interazione cinematica per le costruzioni di classe d'uso III e IV, per sottosuoli di tipo D o peggiori, in siti a sismicità media o alta (ag > 0.25 g). La formula (dovuta a Gazetas) che consente una stima semplificata del momento cinematico da immettere in tabella è riportata nella § 3.3.
Nella tipologia in figura è schematizzato uno strato superiore spesso 1100 cm costituito da argilla normal consolidata per la quale è stato assunto un andamento di Kh che parte da 0 a piano campagna e raggiunge il valore di 55 N/cm³ alla profondità di 1100 cm. Lo strato successivo è di tipo incoerente con un valore costante misurato del modulo Es = 4000 N/cm². Il valore di Kh corrispondente a Es si calcola con la correlazione di Gazetas: Kh=1.2 Es/d = 80 N/cm³ come risulta nella griglia.
Per la stima dei valori Kh si può utilizzare il pulsante 'Stima Kh (per terreni coerenti ed incoerenti)':
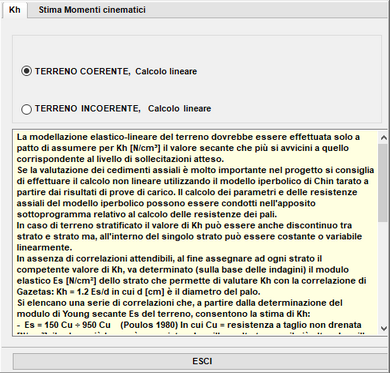
Se la valutazione dei cedimenti assiali è molto importante nel progetto si consiglia di effettuare il calcolo non lineare utilizzando il modello iperbolico di Chin tarato a partire dai risultati di prove di carico. Il calcolo dei parametri e delle resistenze assiali del modello iperbolico possono essere condotti nell'apposito sottoprogramma relativo al calcolo delle resistenze dei pali.
In caso di terreno stratificato il valore di Kh può essere anche discontinuo tra strato e strato ma, all'interno del singolo strato può essere costante o variabile linearmente.
In assenza di correlazioni attendibili, al fine assegnare ad ogni strato il competente valore di Kh, va determinato (sulla base delle indagini) il modulo elastico Es [N/cm²] dello strato che permette di valutare Kh con la correlazione di Gazetas: Kh = 1.2 Es/d in cui d [cm] è il diametro del palo.
Si elencano una serie di correlazioni che, a partire dalla determinazione del modulo di Young secante Es del terreno, consentono la stima di Kh:
- Es = 150 Cu ÷ 950 Cu (Poulos 1980) In cui Cu = resistenza a taglio non drenata [N/cm²]; il valore più basso è associato ad argille molto tenere, il più alto ad argille dure.
- Es = 150 Qu (Poulos 1980) In cui Qu = resistenza in prova CPT [N/cm²].
Secondo Burland & Burbidge (1985) Es può essere stimato attraverso il numero N di colpi ottenuti da prove SPT:
per N = 4 Es [N/cm²] = (1.6 ÷ 2.4) N
per N = 10 Es [N/cm²] = (2.2 ÷ 3.4) N
per N = 30 Es [N/cm²] = (3.7 ÷ 5.6) N
per N = 60 Es [N/cm²] = (4.6 ÷ 7.0) N
Una volta valutato Es si calcola il valore di Kh [N/cm³] da inserire nella grigia dei dati: Kh=Es*d/1.2.
Per gli strati di terreni argillosi uniformi sovraconsolidati si utilizzano i valori di Kh sopra determinati considerandoli costanti (si assegna quindi un solo strato di terreno). Per depositi argillosi uniformi normalconsolidati si considera di solito il valore di Kh come linearmente variabile (assegnando anche in questo caso un unico strato di terreno) con la profondità secondo la seguente relazione (Reese e Matlock 1956):
- Kh = Nh z/d In cui Nh = gradiente di incremento [N/cm³]del coeff. Kh; z = profondità in cm; d = diametro palo in cm."
Valori orientativi di Nh sono forniti da Viggiani (1992):
Argilla normalconsolidata: Nh = 2.0 ÷ 35.0 N/cm³
Argilla organica n.c.: Nh = 1.0 ÷ 8.0 N/cm³
Torba: Nh = 0.3 ÷ 1.0 N/cm³
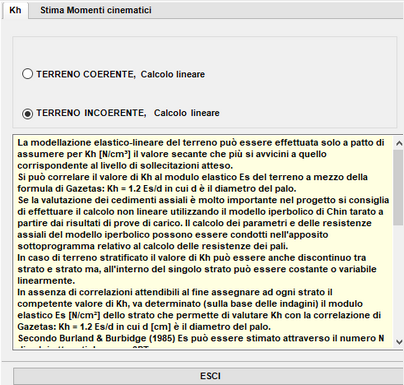
La modellazione elastico-lineare del terreno può essere effettuata solo a patto di assumere per Kh [N/cm³] il valore secante che più si avvicini a quello corrispondente al livello di sollecitazioni atteso. Si può correlare il valore di Kh al modulo elastico Es del terreno a mezzo della formula di Gazetas: Kh = 1.2 Es/d in cui d è il diametro del palo.
Se la valutazione dei cedimenti assiali è molto importante nel progetto si consiglia di effettuare il calcolo non lineare utilizzando il modello iperbolico di Chin tarato a partire dai risultati di prove di carico. Il calcolo dei parametri e delle resistenze assiali del modello iperbolico possono essere condotti nell'apposito sottoprogramma relativo al calcolo delle resistenze dei pali.
In caso di terreno stratificato il valore di Kh può essere anche discontinuo tra strato e strato ma, all'interno del singolo strato può essere costante o variabile linearmente. In assenza di correlazioni attendibili al fine assegnare ad ogni strato il competente valore di Kh, va determinato (sulla base delle indagini) il modulo elastico Es [N/cm²] dello strato che permette di valutare Kh con la correlazione di Gazetas: Kh = 1.2 Es/d in cui d [cm] è il diametro del palo.
Secondo Burland & Burbidge (1985) Es può essere stimato attraverso il numero N di colpi ottenuti da prove SPT:
per N = 4 Es [N/mm²] = (1.6 ÷ 2.4) N
per N = 10 Es [N/mm²] = (2.2 ÷ 3.4) N
per N = 30 Es [N/mm²] = (3.7 ÷ 5.6) N
per N = 60 Es [N/mm²] = (4.6 ÷ 7.0) N
Sempre sulla base di prove penetrometriche SPT è possibile determinare alle varie profondità il valore del modulo elastico Es ad esempio con la correlazione di Schmertman:
Es [N/mm²] = 0.2 B N in cui B=4 per sabbie fini: B= 6 per sabbie medie; B= 10 per sabbie grosse.
Per gli strati di terreni incoerenti uniformi si considera di solito il valore di Kh come linearmente variabile con la profondità secondo la seguente relazione (Reese e Matlock 1956):
Kh = Nh z/d In cui z = profondità in cm; d = diametro palo in cm.; Nh = gradiente di incremento [N/cm³]del coeff. Kh calcolabile attraverso la seguente relazione di Terzaghi (1955):
Nh = A g/1,35 in cui la costante A (adimensionale) tiene conto dello stato di addensamento; g=peso dell'unità di volume [N/cm³]." & vbNewLine
Valori orientativi di A ed Nh sono forniti Terzaghi (1955):
Sabbie sciolte non immerse: A=200; Nh = 2,5 N/cm³
Sabbie sciolte immerse: A=200; Nh = 1,5 N/cm³
Sabbie medie non immerse: A=600; Nh = 7,5 N/cm³
Sabbie medie immerse: A=600; Nh = 5 N/cm³
Sabbie dense non immerse: A=1500; Nh = 20 N/cm³
Sabbie dense immerse: A=1500; Nh = 12 N/cm³
Portanza prevalentemente laterale
E' il caso dei pali totalmente immersi in terreno tendenzialmente omogeneo per cui la rigidezza alla base non è molto differente da quella laterale Questa circostanza viene utilizzata ai fini del calcolo della rigidezza assiale (cedimenti verticali) nella relazione di Randolph e Wroth (1978) (cfr. § 3.3).
Sensibile portanza di base
Se il terreno sotto la base del palo ha una rigidezza superiore a quella media del terreno lungo il fusto va indicato il rapporto tra il modulo elastico G del terreno sotto la base e quello laterale medio (sempre ai fini delle rigidezza assiale e relativi cedimenti valutati con la relazione di Randolph e Wroth).
Resistenza assiale di progetto (al netto del peso proprio)
E' la resistenza di progetto del palo per carichi assiali. Nel caso di una tipologia relativa a pali in gruppo come resistenza di progetto va indicata la resistenza caratteristica. Va valutata a parte. Per pali trivellati e micropali sono stati predisposti appositi programmi di servizio (§ 4.4) tenendo conto dei fattori di correlazione indicati nel § 6.4.3.1.1 delle NTC. La resistenza assiale di progetto può essere valutata sia analiticamente che a mezzo di prove di carico. Detta resistenza di progetto deve essere espressa al netto del peso proprio del palo (§ 6.4.3 NTC). Gli effetti dell'eventuale attrito negativo (calcolati separatamente) possono essere considerati come ulteriori carichi verticali da aggiungere nei nodi di fondazione sede dei pali con attrito negativo.
Resistenza trasversale di progetto SLU
Molto importante nelle combinazioni sismiche, può essere valutata (separatamente) con la teoria di Broms utilizzando ad esempio l'apposito programma di servizio (§ 4.5) oppure, in modo più coerente, secondo il criterio illustrato nell'Esempio 3.
Stima momenti cinematici
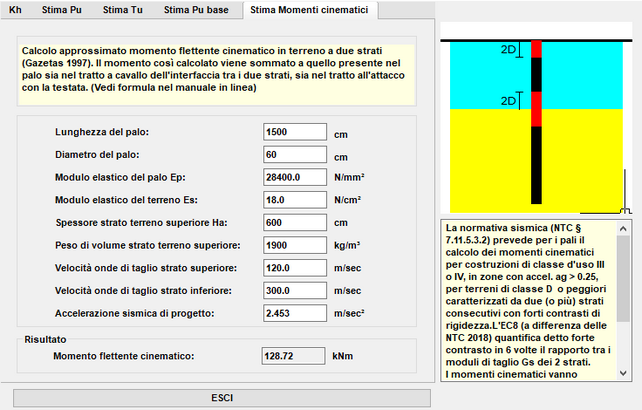
La normativa sismica (NTC § 7.11.5.3.2) prevede per i pali il calcolo dei momenti cinematici per costruzioni di classe d'uso III o IV, in zone con accel. ag > 0.25, per terreni di classe D o peggiori caratterizzati da due (o più) strati consecutivi con forti contrasti di rigidezza.L'EC8 (a differenza delle NTC 2018) quantifica detto forte contrasto in 6 volte il rapporto tra i moduli di taglio Gs dei 2 strati. La formula utilizzata è esposta nel §3.3.
I momenti cinematici vanno sommati a quelli prodotti dal calcolo per tratti di 2 volte il diametro del palo sopra e sotto il confine dei due strati ed all'attacco tra il palo e la testata.
TIPOLOGIE PALI ALLA WINKLER con terreno non lineare
A causa della forte non linearità del terreno questa tipologia di palo è più adatta per una valutazione degli sforzi e delle deformazioni prodotti dalle forze orizzontali (tipicamente quelle sismiche). Per i calcolo dei cedimenti assiali in esercizio si consiglia, invece, la modellazione non lineare di Chin da assegnare sempre nei Dati Generali
Come nel modello lineare il terreno può essere suddiviso in strati orizzontali ed il palo viene suddiviso in conci con molle nei nodi che qui sono non lineari sia in senso assiale (curve t-z) che trasversale (curve p-y). L'andamento dei queste curve lungo la lunghezza del palo dovrebbero derivare da prove su pali pilota strumentati a questo scopo. In questo programma le curve costitutive dei legami sforzi-spostamenti sono di tipo iperbolico e vendono derivate a partire dai parametri geotecnici rilevati nelle indagini.
Per questa tipologia è possibile richiedere (nei Dati Generali) sia il calcolo dell'interazione trasversale tra i pali (da inserire nel calcolo delle combinazioni SLU/SLV) che quello dell'interazione assiale(da inserire nel calcolo delle combinazioni SLE).
Per ognuna delle tipologie di pali (identificata con un qualsiasi nome) vanno assegnati gli ulteriori dati visibili nella sottostante figura.
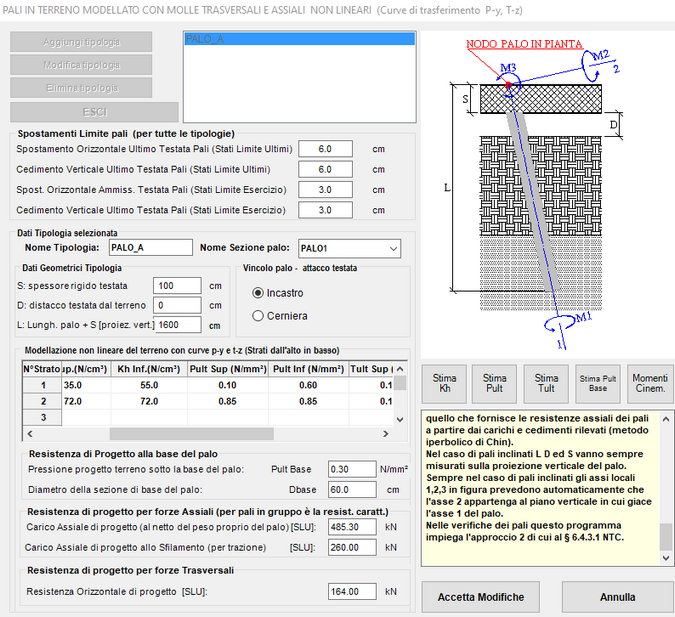
Nella griglia di input, per ogni strato, vanno assegnati i valori i valori iniziali e finali di Kh (rigidezza elastica all'origine), Pult (pressione traversale asintotica sopportabile dal terreno), Tult (tensione tangenziale assiale asintotica del terreno lungo il fusto). Detti valori possono essere ricavate a partire da prove di carico su pali appositamente strumentati o da relazioni analitiche basate su parametri geotecnici rilevati nelle indagini.
Le resistenze assiali e trasversali di progetto (al netto del peso proprio del palo) ed orizzontali dei pali vanno assegnate direttamente dall'utente. Per la loro determinazione si vedano i punti 6.4.3.1.1 e 6.4.3.1.2 NTC in cui possono essere stimati statisticamente (e ridotti mediante coeff. parziali di sicurezza R3, sia a mezzo di prove di carico sia con metodi analitici o relazione empiriche (sempre basati su parametri geotecnici rilevati in sito).
In assenza delle prove di carico dirette su pali, per una valutazione analitica di dette resistenze di progetto (basate solo sui parametri geotecnici stimati sulla base delle verticali di indagine) possono impiegarsi gli appositi programmi di servizio selezionabili dal menu generale. Nel caso si siano effettuate prove di carico su pali pilota, tra i programmi di servizio è presente quello che fornisce le resistenze assiali dei pali a partire dai carichi e cedimenti rilevati (metodo iperbolico di Chin).
Nel caso di pali inclinati L D ed S vanno sempre misurati sulla proiezione verticale del palo. Sempre nel caso di pali inclinati gli assi locali 1,2,3 in figura prevedono automaticamente che l'asse 2 appartenga al piano verticale in cui giace l'asse 1 del palo.
Nelle verifiche dei pali questo programma impiega l'approccio 2 di cui al § 6.4.3.1 NTC.
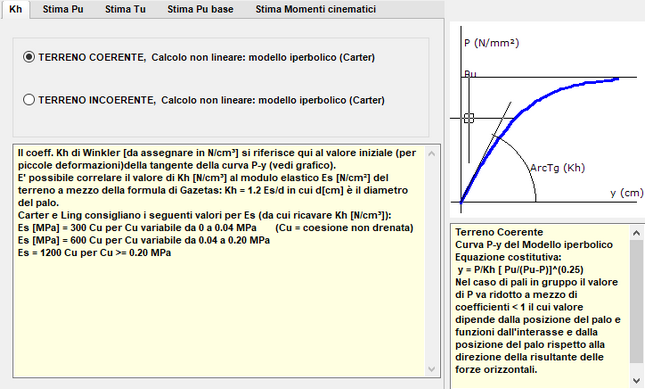
I coeff. Kh di winkler trasversali da immettere corrispondono alla tangente all'origine della curva iperbolica p-y (per piccole deformazioni). I criteri di calcolo dei coeff. Kh sono descritti nella finestra di dialogo sottostante che sia apre tramite il pulsante apposito.
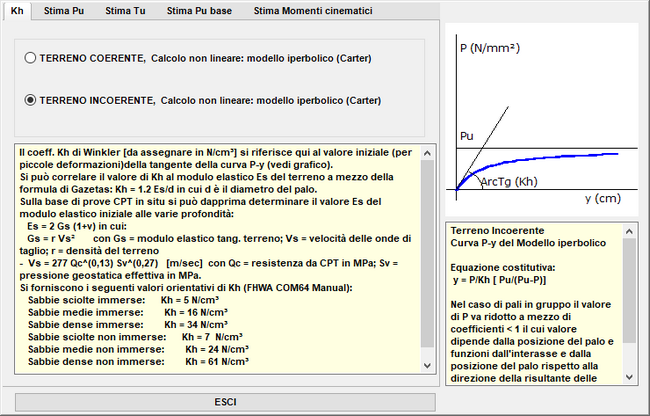
Per l'interazione tangenziale lungo il fusto sono anche previste due curve costitutive non lineari.Le tensioni tangenziali Tult Sup, Tult Inf, sono quelle limiti che assicurano la portanza assiale laterale del palo (vedi la seguente finestra di dialogo selezionabile col pulsante "Stima Tult":

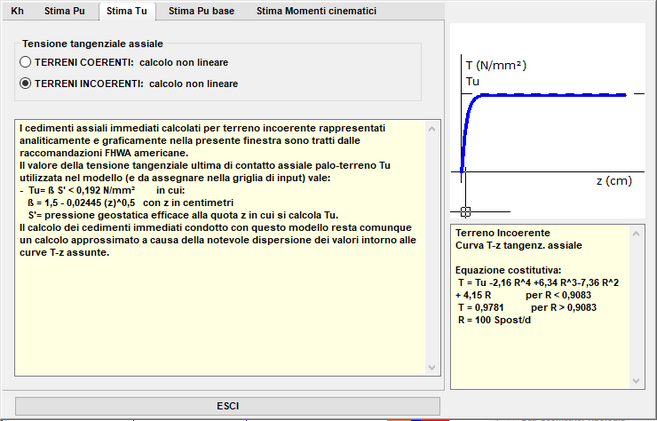
Per la reazione assiale non lineare della base del palo è prevista la seguente schematizzazione (sempre ad andamento iperbolico):
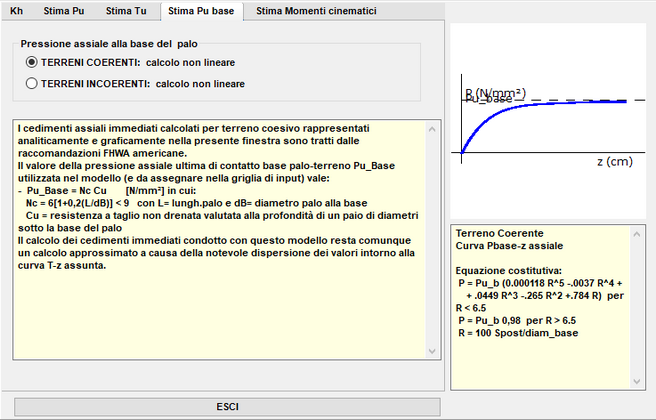
TIPOLOGIE PALI ASSIALMENTE NON LINEARI CON MODELLO IPERBOLICO (CHIN)
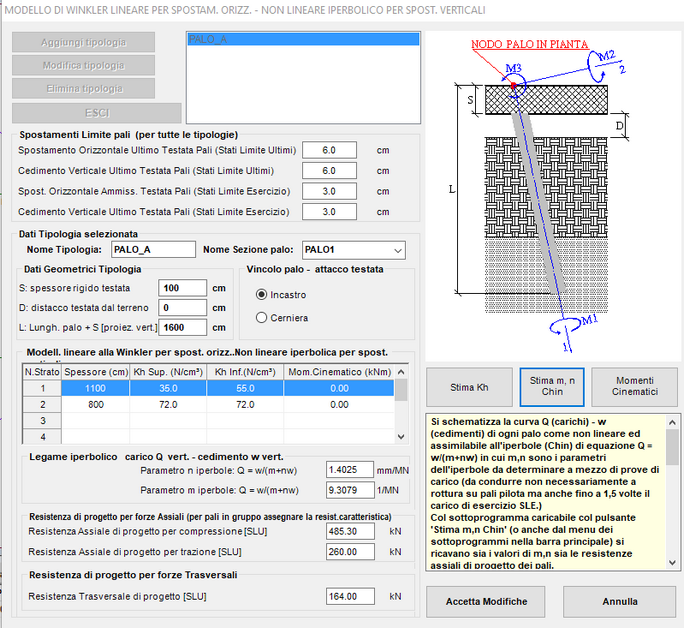
Questa tipologia è particolarmente adatta per una valutazione più affidabile dei cedimenti assiali nelle combinazioni di esercizio SLE specialmente in presenza di pali in gruppo e (in questo caso) unitamente alla messa in conto dell'interazione assiale tra i pali. Questo modello prevede che la curva costitutiva carichiQ) - cedimenti(w) del palo abbia un andamento iperbolico (evidenza sperimentale quasi sempre verificata nelle prove su pali):

L'equazione parametrica dell'iperbole di Chin (in figura) é: Q = w / (m + w·n)
Il significato fisico del parametro m (utilizzato in programma e da assegnare nell'Archivio tipologie pali) è costituito dall'inverso della tangente iniziale dell'iperbole: m= 1/KI
Il significato fisico del parametro n (utilizzato in programma e da assegnare nell'Archivio tipologie pali) ) è costituito dall'inverso del larico limite asintotico Qlim: n=1/Qlim
L'utilizzo di questo modello è quindi particolarmente indicato nel caso in cui si effettuino prove di carico su pali pilota fino a rottura. Le NTC definiscono la rottura assiale di un palo quella corrispondente ad un cedimento w pari al 10% del diamtero del palo, per pali fini a 80 cm di diametro e pari al 5% del diametro per pali di maggiore diametro. Di conseguenza il carico limite da utilizzare per le verifiche di resistenza assiali GEO non è quello sopra indicato ma è quello corrispondente al cedimento limite di normativa w:
Qlim* = w / (m + w · n)
Una volta calcolato Qlim* può dedursi la resistenza caratteristica e quella di progetto da impiegare per le verifiche GEO assiali del palo. Ad esempio nel caso della tipologia sopra illustrata il valore asintotico della resistenza limite sarebbe pari a Qlim = 1/ n = 1/1.4025 = 0.7130 MN. Assumendo per w il valore di normativa w =0.1 d = 60 mm il carico limite di normativa da assumere in progetto si riduce a:
Qlim* = 0.642 MN.
Il carico limite caratteristico (con una sola prova diretta) è Qk = 0.642 / 1.4 = 0.4585 = 458.5 kN. Il carico limite di progetto è: Qd = Qk / 1.3 = 0.352 MN = 352 kN (R3=1.3 senza distinzione tra resistenza alla punta e laterale). Nel caso in cui la tipologia in discussione appartenga a pali in gruppo come carico limite di progetto Qd può impiegarsi il suo valore caratteristico Qk.
Una volta conseguiti con prove di carico la serie di valori di Q e w è immediato ottenere i parametri m,n,Qd a mezzo del programma di servizio: Resistenza a compressione palo da prove di carico.
Anche con prove dirette non distruttive che si spingano a carichi dell'ordine di una volta e mezzo i valori di esercizio, possono ottenersi eccellenti valutazioni sia carico ultimo assiale (da cui dedurre quello di progetto) sia dei parametri dell'iperbole rappresentativa dell curva carichi-cedimenti. I parametri m, n della suddetta iperbole di equazione Q = w/(m+nw) possono essere calcolati con l'apposito programma di servizio (§ 4.4) in cui vengono stimati anche le resistenze caratteristiche e di progetto del palo (anche nel caso di prove di collaudo).
Nell'impossibilità di effettuazione delle prove dirette i parametri m, n possono essere stimati (ma con minore attendibilità) anche a partire da una valutazione separata ed analitica della resistenza ultima basata sui valori geotecnici ottenuti nelle verticali di indagine. (cfr. § 3.3).
Nella presente tipologia Il calcolo delle rigidezze trasversali dei pali è, invece, lineare ed è effettuato con le stesse modalità ed a partire dagli stessi dati descritti per la precedente tipologia alla Winkler lineare.
Geostru Software ©