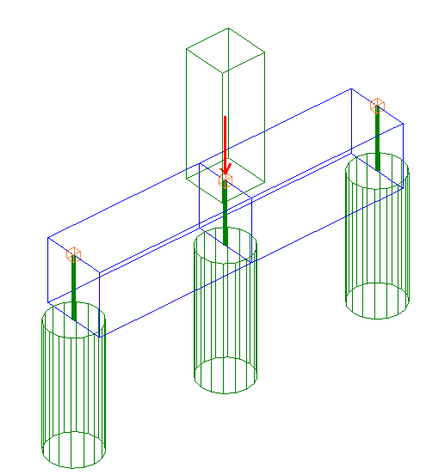
Questo esempio è volto ad illustrare gli effetti allo SLE dell'interazione assiale tra i pali (§ 3.3) tenendo conto della non linearità della curva carichi-cedimenti del terreno con il metodo iperbolico di Chin.
La semplicità dello schema prescelto è utile per evidenziare la complessità del problema.
Per utilizzare al meglio il metodo iperbolico di Chin è necessario disporre di almeno una prova di carico su palo pilota (o su palo di prova). In questo caso a partire dalle misure carichi-cedimenti rilevate (su di un unico palo pilota o a valle di una prova di collaudo) ed utilizzando il programma di servizio di cui al § 4.3, si sono ottenuti i seguenti dati di partenza per i tre pali dell'esempio:
d = 80 cm = diametro palo trivellato con calcestruzzo classe C28/35
L = 2450 cm = lunghezza del palo (2350) + spessore testata (100)
m = 0.7716 mm/MN = parametro m dell'iperbole di equazione Q = w / (m+n w)
n = 0.135 MN = parametro n dell'iperbole
Rc =7337,00 kN = Carico assiale di collasso geotecnico (§ 6.4.3.7.1 NTC) = 0.1·d /(m+ 0.1·d ·n)
Rk = 7337/1.4=5241 kN = Resistenza caratteristica (tabella 6.4.III NTC 2018 con una sola verticale di indagine)
Rd = 5241 kN = Resistenza di progetto (= Resistenza caratteristica per pali in gruppo)
Si è ipotizzata la presenza di un unico carico verticale di 7500 kN agente al centro della trave di collegamento. In un semplice schema di comportamento alla Winkler dei pali e con trave di testata infinitamente rigida si dedurrebbe subito che i tre pali sarebbero sottoposti ad un uguale carico verticale pari a 7500/3 = 2500kN.
In un primo Esempio (file ESEMPIO_8_1.f3f) il calcolo viene svolto tenendo conto delle reali rigidezze della trave di collegamento avente sezione 100x100 cm e dei pali. Si deterninano cioè, considerando la non linearità dei cedimenti assiali e l'interazione assiale tra i pali, quali sono le probabili sollecitazioni ed i cedimenti assumendo una trave di collegamento avente dimensioni di 100x100 cm.
In un secondo esempio (file ESEMPIO_8_2.f3f) viene, a parità di carico, assunta una trave di collegamento pressochè infinitamente rigida a flessione.
Nel terzo esempio (file ESEMPIO_8_3.f3f) lo stesso schema, sottoposto anche a forza orizzontale SLV, verrà calcolato con le curve non lineari di trasferimento p-y e l'interazione orizzontale (metodo dei P-moltiplicatori).
ESEMPIO 8.1
Con la trave di collegamento 100x100 cm si sono svolte due distinte calcolazioni: la prima in assenza di interazione, la seconda con interazione (selezionando o meno la casella di scelta nei Dati generali).
I risulati dei due calcoli sono:
Htrave = 100 cm
3401.47 kN / 0,492 cm Carico / Cedimento Palo Centrale SENZA INTERAZIONE
2049,27Kn / 0,218 cm Carico / Cedimento Pali Laterali SENZA INTERAZIONE
3729,64 kN / 1,011 cm Carico / Cedimento Palo Centrale CON INTERAZIONE
1885,18 Kn / 0,755 cm Carico / Cedimento Pali Laterali CON INTERAZIONE
La deformabilità della trave di collegamento (non molto rigida) determina una notevole differenza tra i carichi trasmessi ai pali laterali rispetto a quello del palo centrale. Nel caso di presa in conto dell'interazione questa differenza si accentua ulteriormente nonostante l'interazione tenda a scaricare i pali interni. Si noti inoltre che il cedimento del palo centrale in caso di interazione sia circa il doppio di quello calcolato in assenza di interazione. Forti sforzi di flessione e taglio vengono a determinarsi nella trave e nei pali per effetto delle deformazioni (sforzi non valutabili nel semplice schema lineare alla Winkler con testata indeformabile).
ESEMPIO 8.2
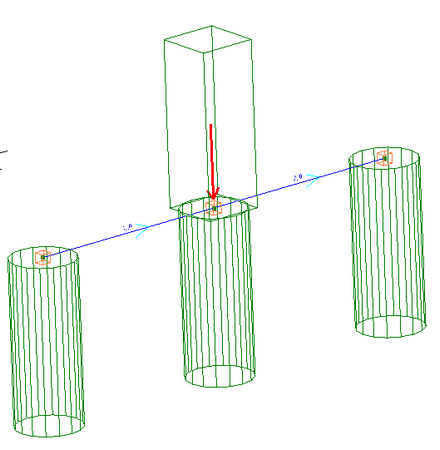
Si consideri ora il caso in cui gli stessi tre pali dell'esempio 8.1 siano collegati da una testata infinitamente rigida come quella costituita da una pila da ponte sotto la quale siano attestati i pali. In questo caso detta testata può essere modellata mediante una trave di collegamento la cui sezione va definita nell'Archivio travi-pali come sezione di forma di 'Generica per dati' (in questo esempio il nome assegnato a questa sezione è 'RIG') . Si è, cioè, assegnato un altissimo valore all'inerzia Jz, escludendo la deformazione a taglio nei Dati Generali. Nell'archivio tipologie pali si è annullato lo spessore della testata e ridotta la lunghezza L a quella netta del palo di 2350 cm.
Anche in questo esempio si sono svolte due distinte calcolazioni: la prima in assenza di interazione, la seconda con interazione.
I risulati dei due calcoli sono:
2500,00 kN / 0.291 cm Carico / Cedimento Palo Centrale SENZA INTERAZIONE
2500,00 Kn / 0,291cm Carico / Cedimento Pali Laterali SENZA INTERAZIONE
1747,97 kN / 0.807 cm Carico / Cedimento Palo Centrale CON INTERAZIONE
2873,0 Kn / 0,807 cm Carico / Cedimento Pali Laterali CON INTERAZIONE
La infinita rigidezza della trave di collegamento non determina differenza alcuna tra i carichi assiali trasmessi ai pali laterali rispetto a quello del palo centrale. Nel caso di presa in conto dell'interazione si verifica, invece, la circostanza che i carichi assiali nei pali laterali risultino molto superiori a quello trasmesso nel palo centrale. Anche qui i cedimenti risultano uguali per i tre pali ma molto maggiori in valore assoluto per effetto dell'interazione.
Escludendo il caso dei pali attestati sotto pile da ponte, si può quindi concludere che la messa in conto della deformabilità della testata di collegamento dei pali è di grande importanza nella previsione della ripartizione dei carichi assiali tra i pali in gruppo e, di conseguenza, sulla valutazione degli sforzi e delle armature dei pali e della testata.Tali valutazioni non sarebbero corrette se si utilizzasse, in ogni caso, l’ipotesi di infinita rigidezza della testata come assunta in alcuni programmi.
Esempio 8.3
Allo schema precedente dell'esempio 8.2 viene aggiunto un carico orizzontale H= 480 kN sempre proveniente dal pilastro centrale.
Per questo schema dominato dalla intensità delle forze orizzontali si adotta la modellazione del terreno non lineare basata sulle curve di trasferimento p-y. Trattandosi di terreno incoerente la pressione laterale ultima del terreno nel primo strato convenzionale profondo 3 d = 240 cm viene assegnata linearmente crescente da 0 a 0.048 N/mm²; quella dalla profondità di 240 cm a 2350 cm varia linearmente da 0.048 a 0.42 N/mm².
E' necessario preventivamente calcolare la resistenza orizzontale di progetto del singolo palo. Trattandosi di un elevato carico orizzontale si prevede un comportamento duttile del palo in modo da poter applicare la teoria di Broms per il calcolo di detta resistenza. Cioè occorrerà armare il singolo palo con un'armatura longitudinale pari ad almeno l'1% dell'area della sezione del palo (§7.5 NTC). Utilizzando l'apposito programma di servizio (calcolo resistenza trasversale palo trivellato con Broms) si ottiene una resistenza di progetto di 253 kN se si arma il palo con almeno 18F20 (1.1%Ac). Questo minimo di armatura va inserita nell'archivio dati sezioni/pali in corrispondenza della sezione circolare del palo in esame.
In uno schema di calcolo privo di interazione trasversale tra i pali per forze orizzontali il carico H = 480 kN verrebbe ripartito nella stessa misura tra i tre pali (Hi = 480/3 = 160 kN).
L'interazione assegnata, invece, produce una differente ripartizione della forza H producendo un maggiore carico H3 = 184.80 kN sul palo P3_0 rispetto ad esempio palo P1_0 sul quale agisce il carico H1 = 139.75 kN.
Queste differenti forze orizzontali conducono a maggiori sforzi di momento e taglio in alcuni pali rispetto a quelli che si otterrebbero con una ripartizione media senza interazione trasversale tra i pali.
La relazione di calcolo delle verifiche geotecniche dei pali fornita dal programma (vengono anche indicati i moltiplicatori delle curve p-y che, per i suddetti pali, valgono rispettivamente 0.856 e 0.665) è, pertanto, la seguente:
RISULTATI VERIFICHE PALI
VERIFICA (GEO) RESISTENZA ASSIALE DI GRUPPO PER I PALI NON APPARTENENTI A PLINTI
Coeff. Eff. Coefficiente di Efficienza (<=1) del gruppo di pali assegnata in funzione della geometria e del tipo di terreno
Carico Tot. kN Somma di tutti i carichi assiali agenti sui pali per la combinazione in esame
Car.Lim.Gruppo kN Coeff.Effic. x la somma dei carichi assiali ultimi dei pali
Sicurezza Rapporto tra il carico limite del gruppo di pali del plinto e il relativo carico totale (OK se >=1)
Coeff. Eff. Comb. Ver(S/N) Carico Tot. Car.Lim.Gruppo Sicurezza
0.900 1^ (SLU) S 5000.00 10881.00 2.176
VERIFICA RESISTENZA PER CARICHI TRASVERSALI DI GRUPPO PER I PALI NON APPARTENENTI A PLINTI
Effic.V Efficienza (<=1)trasversale del gruppo di pali assegnata in funzione della geometria e del tipo di terreno
Carico Tot. kN Somma di tutti i carichi trasversali agenti sui pali per la combin. in esame
Car.Lim.Gruppo kN Efficienza x la somma dei carichi trasvers. di progetto dei pali
Sicurezza Rapporto tra il carico trasv. totale di progetto dei pali e il carico totale (OK se >=1)
Effic.H Comb. Ver(S/N) Carico Tot. Car.Lim.Gruppo Sicurezza
0.900 1^ (SLU) S 480.00 531.30 1.107
SPOSTAMENTI DELLA TESTA DEI PALI PER LE SINGOLE COMBINAZIONI DI CARICO
Plinto Nodo centrale del Plinto su pali cui appartiene il palo corrente
Sp.X / Sp.Y / Sp.Z cm Spostamenti in cm della testa del palo nel sist. gen. di riferimento X,Y,Z
Rot.X / Rot.Y/ Rot.Z Rad Rotazioni della testa del palo intorno agli assi X,Y,Z del riferimento generale
P-y Coeff. Coeff. riduttivi della rigidezza alla traslazione orizz. dei pali per interazione di gruppo tra i pali (abaco di Mokwa)
COMBINAZIONE DI CARICO 1^ (SLU)
NodoPalo Plinto Sp.X Sp.Y Sp.Z Rot.X Rot.Y Rot.Z P-y Coeff.
P1_0 ---- 0.929 0.000 -0.142 0.00000 0.00014 0.00000 0.665
P2_0 ---- 0.929 0.000 -0.176 0.00000 0.00014 0.00000 0.736
P3_0 ---- 0.929 0.000 -0.210 0.00000 0.00014 0.00000 0.856
VERIFICHE GEOTECNICHE DEGLI SFORZI IN TESTA DEI PALI (PER OGNI COMBINAZIONE)
N.B. gli sforzi sono riferiti agli assi locali del palo:
Asse x = asse longitudinale baricentrico del palo.
Asse y = asse locale sezione di testa parallela all'asse Y generale se il palo è verticale;
nel caso di palo inclinato esso giace nel piano verticale contenente l'asse x locale.
Asse z = asse orizzontale ortogonale agli assi x, y secondo la regola della mano destra.
N kN Sforzo normale (positivo se di compressione) nella sezione di attacco del palo (testa)
Nd kN Carico assiale di progetto (in compressione o trazione) assegnato alla tipologia del palo
V kN Taglio [vettoriale sqr(Ty²+Tz²)] nella sezione di attacco del palo (testa)
Vd kN Carico trasversale di progetto assegnato alla tipologia del palo
COMBINAZIONE DI CARICO 1^ (SLU)
NodoPalo Plinto N Nd V Vd
P1_0 ---- 1375.21 4030.00 139.75 253.00
P2_0 ---- 1671.44 4030.00 155.45 253.00
P3_0 ---- 1953.35 4030.00 184.80 253.00