El modelo denominado CRSP (Colorado Rockfall Simulation Program) fue desarrollado por Pfeiffer y Bowen (1989) con el objeto de modelar el movimiento de la caída de bloques en forma de esfera, de cilindro o de disco, con sección circular en el plano vertical del movimiento.
Para describir el movimiento de los bloques, este modelo aplica la ecuación del movimiento parabólico de un cuerpo en caída libre y el principio de conservación de la energía total.
El fenómeno del impacto se modela utilizando como parámetros ulteriores, respecto al método Lumped mass, la rugosidad del talud y la dimensión de los bloques.
El modelo CRSP asume que el ángulo formado entre la dirección del bloque y el perfil del talud varía según estadísticas que se deben definir en cada caso analizado. Por lo tanto el modelo trata los resultados estadísticamente y los mismos consisten principalmente en las velocidades y las alturas de rebote con respecto a la superficie del talud durante la caída. Por consiguiente considera las combinaciones de los movimientos de caída libre, rebote, rodadura y deslizamiento que pueden variar según las dimensiones de los bloques y de la rugosidad del talud.
La confiabilidad del modelo ha sido verificada por medio de comparaciones entre los resultados numéricos y los obtenidos en pruebas in situ.
La descripción del movimiento en caída libre inicia en un punto en el cual se conoce la velocidad inicial descompuesta en componente horizontal y vertical. El bloque es sometido al movimiento de caída libre hasta que colisione con la superficie del talud.
De la intersección se recaban las coordenadas del punto del impacto. El vector de la velocidad de pre impacto V, forma un ángulo α con el talud.
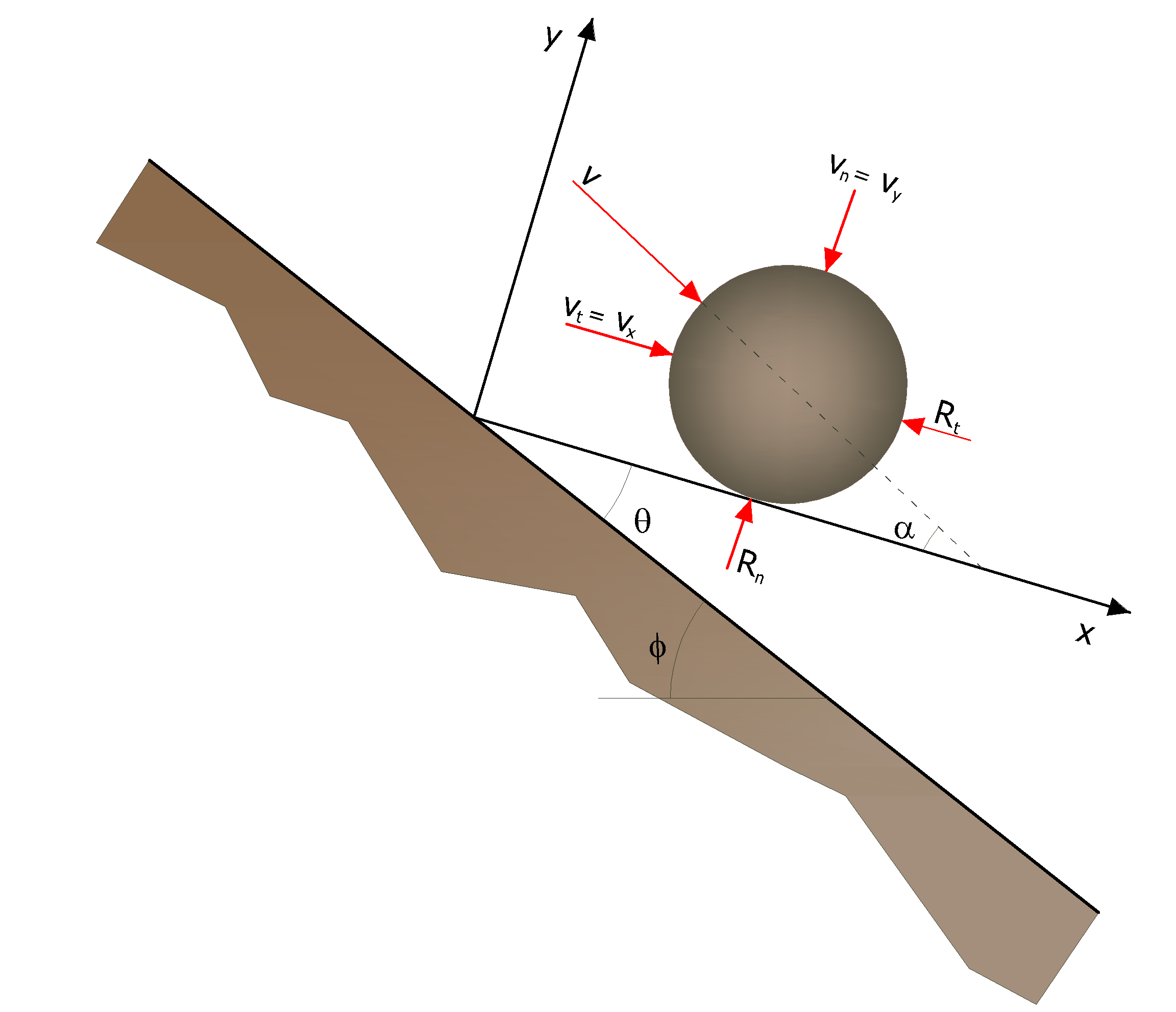
A cada impacto la inclinación del talud f se hace cambiar casualmente en un rango de valores comprendido entre 0 y θmáx. el valor de θmáx
depende de la rugosidad del talud y de la dimensión del bloque y se determina con medidas in situ.
Con R como radio del bloque en examen se tiene:
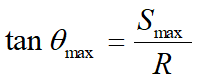
El ángulo θmax se define como la máxima variación de la línea de pendencia promedio con respecto al radio R de la roca.
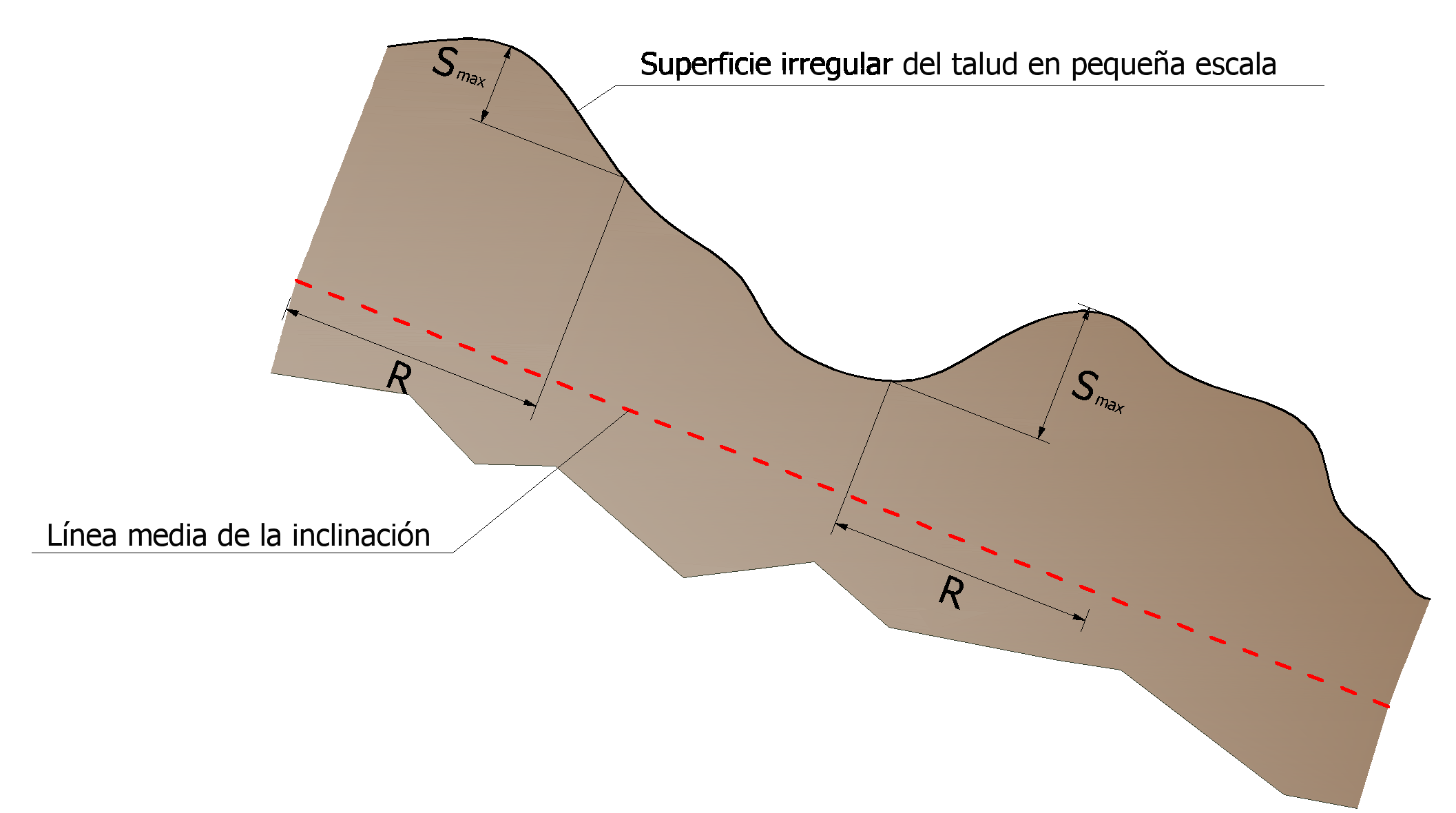
La velocidad que se obtiene después del impacto se determina por medio de la ecuación de conservación de la energía total:
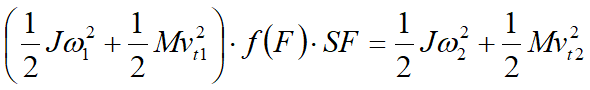
donde:
R Radio del bloque;
M Masa del bloque;
J Momento de inercia del bloque;
ω1 Velocidad angular antes del impacto;
ω2 Velocidad angular después del impacto;
Vt1 Velocidad tangencial antes del impacto;
Vt2 Velocidad tangencial después del impacto.
La función f(F) de rozamiento viene así definida:
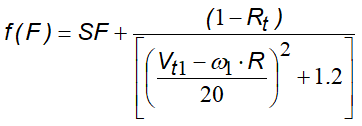
Mientras la función de escala SF:
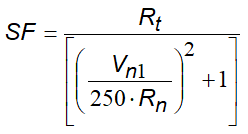
Los términos f(F) y SF se obtienen a través de expresiones empíricas que se utilizan para valorar la energía cinética disipada en las colisiones entre bloque y talud a causa del rozamiento y del choque.
El rozamiento tiene que ver principalmente con la disipación de la energía producida por la velocidad tangencial, mientras que el choque tiene que ver con aquella producida por la velocidad normal al talud.
Las velocidades tangenciales y angulares post colisión entran en relación entre ellas con la siguiente ecuación:
![]()
que asume que los bloques abandonan el contacto con el talud rodando, independientemente de la velocidad angular precedente.
La velocidad normal post colisión se obtiene de la siguiente expresión empírica:
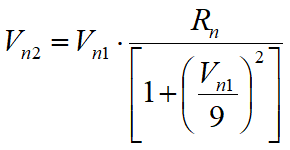
que trata de tener en cuenta el hecho, verificado también experimentalmente, que la relación entre las velocidades normales post impacto y pre impacto disminuye con el aumento de la misma velocidad normal pre impacto.
Rn Coeficientes de restitución normal;
Rt Coeficientes de restitución tangencial;
R Radio del bloque.
|
© GEOSTRU- GeoRock 2D