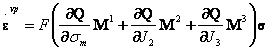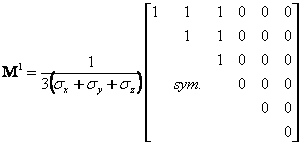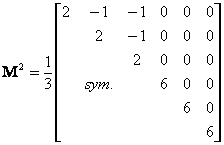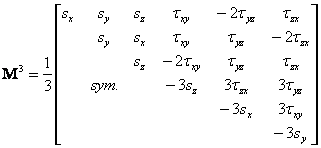Nonlinear analysis formulation > Elastic-plastic procedures > Constant-stiffness method

In this method the material is allowed to sustain stresses outside the failure criterion for finite "periods". Instead of plastic strains, we refer to viscoplastic strains and are generated as a rate that is related to the amount by which yield has been violated by:

(163)

where F is the yield function and Q is the plastic potential function.

The increment of viscoplastic strain, which is accumulated from one iteration to the next, is obtained through multiplication the strain rate by a pseudo time step as:

(164)

and

(165)

where the time step for numerical stability depends on the assumed failure criterion as:

for Von-Misees materials

(166)

for Mohr-Coulomb materials

(167)

The derivatives of the plastic potential function Q with respect to stresses are expressed as:

(168)

where where t represents the second deviatoric stress invariant:

(169)

and

(170)

, etc.

(171)

(179)

where the first invariant (mean stress invariant) s is given by the relation:

(180)

It may be noted that in geotechnical applications, plane strain conditions are enforced and in the above equations .

The viscoplastic strain rate is evaluated numerically by the expression:

p_64_image014

(181)

where

p_64_image016

(182)

p_64_image018

(183)

p_65_image002

(184)

(185)

The self-equilibrating body loads are accumulated at each time step within each load step by summing the following integrals for all yielded elements (F>0 at Gauss points):

(186)

This process is repeated at each time step iteration until no integration point stresses violate the failure criterion within a given tolerance. The convergence criterion is based on a dimensionless measure of the amount by which the displacement increment vector Ui changes from one iteration to other.