<< Click to Display Table of Contents >> Navigation:  Formulation of the element matrices and vectors for elasticity problem > Numerical integration in finite elements

 

Integration of expressions for stiffness matrices and load vectors can not be performed analytically for general case of isoparametric elements. Instead, stiffness matrices and load vectors are typically evaluated numerically using Gauss quadrature rule over triangular or quadrilateral regions. The Gauss quadrature formula for the domain integral in two-dimensional case (natural coordinates) is of the form:

 

 

where , are abscissas and Hi are weighting functions of the Gauss integration rule.

 

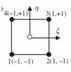
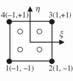
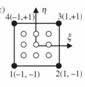
The sampling points and weighting functions used for quadrilateral elements are shown in Table 3.

 

A pattern of either 2 x 2 or 3 x 3 sampling points is used, depending on the order of the function to be evaluated. Generally the four-point formula is used for the 4-noded quadrilateral, while the nine-point formula is used for the 8-noded element.

 

The general 8-node quadrilateral element stiffness matrix contains fourth order polynomial terms and thus requires nine sampling points for exact integration. It is often the case, however, that the use of "reduced" integration by using the four integration points improves the performance of this element. This is found to be particularly true in the plasticity applications.

 

 

         Table 3. Gauss quadrature weights and sampling points for quadrilateral elements.

 

 

 

         Table 4. Gauss quadrature weights and sampling points for triangular elements.

 

 

The weights and quadrature points for triangular elements (constant strain triangle-T3 and linear strain triangle-T6) are summarized in Table 4.

 

 

 

 

 

 

 

 

© GeoStru Software