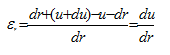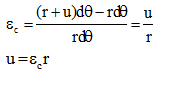Un solido di rivoluzione è un corpo tridimensionale generato per rotazione di una sezione piana attorno ad un asse (Figura 17). Un solido di rivoluzione è assialsimmetrico se le proprietà geometriche e del materiale sono indipendenti dall’anomalia J. Se il carico è anch’esso assialsimmetrico il problema si riduce al caso bidimensionale; ogni punto del mezzo è caratterizzato dagli spostamenti u (radiale) e w (assiale); l’analisi è essenzialmente coincidente con quella del problema piano con la presenza delle componenti circonferenziali della deformazione e della tensione.
Le componenti delle tensioni e deformazioni per l’elemento sono:
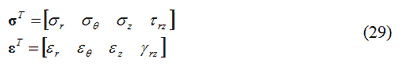
dove le deformazioni sono definite come segue, con u e w che rappresentano gli spostamenti rispettivamente in direzione r e z:
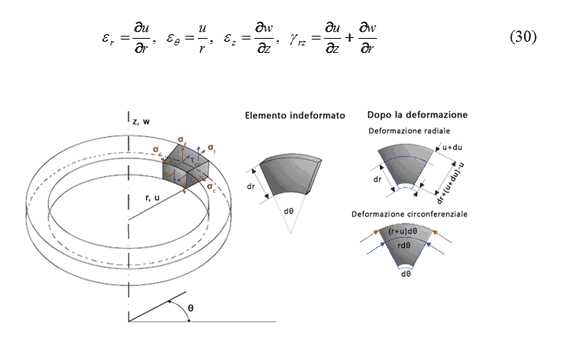
Fig. 17. Elemento assialsimmetrico e rappresentazione della sua deformazione.
Nota:
Deformazione radiale
|
Deformazione circonferenziale
|
|
|
La matrice costitutiva E, che collega le tensioni alle deformazioni, è:
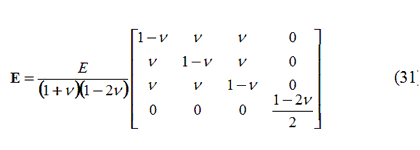
Dove E rappresenta il modulo di Young e ν il rapporto di Poisson.