Gli elementi isoparametrici piani impiegati in GFAS hanno forma triangolare, quadrangolare, lineare o quadratica. La formulazione crea una corrispondenza biunivoca tra un elemento di forma qualsiasi nel sistema cartesiano (x, y) e un elemento di forma semplice nel sistema di riferimento naturale (x, h): ciò è possibile attraverso la definizione di specifiche funzioni di trasformazione o di forma definite nel sistema naturale dell’elemento.
Le funzioni di forma sono utilizzate sia per specificare la forma degli elementi sia per l’interpolazione nel campo degli spostamenti.
Gli spostamenti (u,v) in ogni punto di un elemento piano sono interpolati a partire dagli spostamenti nodali (ui,vi) utilizzando le funzioni di forma Ni come segue:
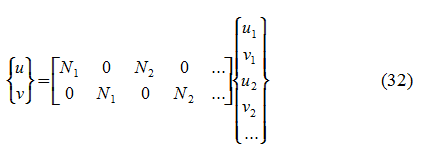
Ovvero:
![]()
Dove N è la matrice funzione di forma, u il vettore spostamento e d il vettore spostamento nodale.
Si assume che u e v siano indipendenti pertanto u dipende solo da u e v dipende solo da v.
Dalla relazione deformazione-spostamento segue che:

avendo posto:

B rappresenta la matrice deformazione-spostamento.
L’ipotesi su cui si poggia la descrizione analitica del comportamento elastico è l’esistenza di un potenziale della deformazione. Si assume cioè che il processo deformativo comporti l’immagazzinamento di un’energia a spese della quale le deformazioni vengono recuperate una volta rimossa la causa deformante.
Tale potenziale detto “energia di deformazione” per ogni elemento, è definito dall’espressione:
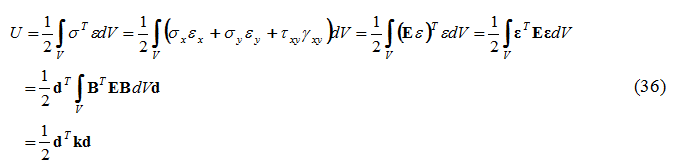
Si ottiene, così, la formula generale della matrice delle rigidezze per gli elementi:

dove la matrice costitutiva E è data dalla relazione tensione-deformazione. La matrice delle rigidezze k, definita dalla formula sopra riportata, è definita simmetrica fintanto che la matrice E è simmetrica.