La Figura 18 mostra l’elemento triangolare bidimensionale semplice, che ha due gradi di libertà per ogni nodo. È detto anche elemento lineare triangolare (Constant Strain Triangle – CST).
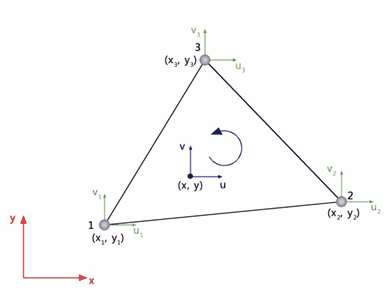
Fig. 18. Elemento finito triangolare lineare (T3).
L’elemento è caratterizzato da 3 nodi ai vertici del triangolo numerati in senso antiorario. Ogni nodo ha due gradi di libertà, pertanto si potrà muovere nella direzione x e y. Per ogni punto interno al triangolo, gli spostamenti u e v sono definiti da funzioni lineari:

Le costanti α e β si determinano imponendo le condizioni di vincolo ai nodi.
Risolvendo il sistema di equazioni si possono ricavare i coefficienti in termini di spostamenti nodali e coordinate.
Ogni elemento può essere rappresentato mediante due sistemi di coordinate: le coordinate globali o del sistema fisico (x, y) e le coordinate locali o del sistema naturale (ξ, η) (Figura 19).
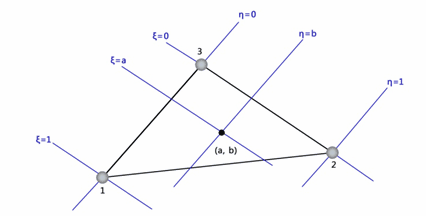
Fig. 19. Coordinate naturali per un elemento finito triangolare lineare.
La relazione che intercorre tra le due è la seguente:
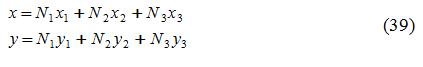
Ni sono le funzioni di forma definite nel sistema naturale (ξ, η) (Figura 19). Le funzioni di forma sono in numero pari ai nodi dell’elemento e variano tra 0 e 1: esse assumono valore 1 in corrispondenza del nodo i di coordinate (xi, yi) e valore nullo in corrispondenza degli altri nodi dell’elemento. Possono essere rappresentate come:
![]()
Così, in funzione dei gradi di libertà nodali, il campo degli spostamenti è definito come:
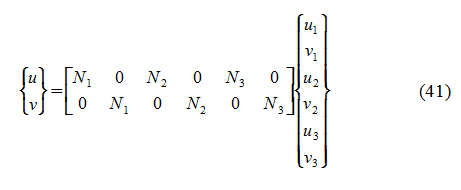
Utilizzando la regola della catena per le derivate, si ha:
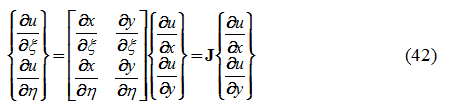
dove J è chiamata matrice Jacobiana della trasformazione.