Questo elemento è anche chiamato elemento triangolare quadratico. È definito da 6 nodi: 3 sono posizionati nei vertici del triangolo e 3 nei punti medi dei lati (Figura 20). Ogni nodo ha due gradi di libertà e gli spostamenti (u, v) sono definiti come funzioni quadratiche di (x, y).
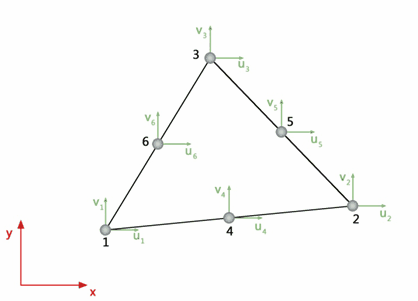
Fig.20. Elemento triangolare quadratico.
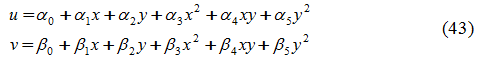
Da ciò si ha che le deformazioni sono funzioni lineari, perciò il triangolo è definito a deformazione lineare ( Linear Strain Triangle – LST) ed è pertanto in grado di fornire risultati migliori rispetto al triangolo a deformazione costante (CST).
Nel sistema di coordinate naturali, si definiscono facilmente le sei funzioni di forma per l’elemento LST come:

In cui ![]()
Gli spostamenti posso essere formulati come:

Gli elementi della matrice delle rigidezze sono dunque dati da:

Dove il prodotto BTEB è un prodotto quadratico in x e y, e l’integrale è computabile numericamente.