Există situaţii în care nu este posibilă menţinerea rezultantei presiunilor asupra terenului în interiorul treimii mijlocii a bazei fundaţiei.
Această situaţie se manifestă când una sau mai multe combinaţii de sarcini depăşesc substanţial capacitatea fundaţiei de a se opune la momentul de răsturnare (condiţii de sarcină tranzitorii sau temporare datorate vântului sau seismului).
Deşi fundaţiile nu sunt de obicei proiectate pentru astfel de condiţii de sarcină, stabilitatea lor la răsturnare ar trebui verificată în prezenţa acestor sarcini temporare.
Inginerul geotehnic ar trebui să poată furniza, la solicitarea clientului, un calcul separat al presiunii admisibile pe teren q'0 validă pentru condiţiile de sarcină temporare, alta decât cea de utilizată pentru condiţiile de exerciţiu.
Pentru o excentricitate

faţă de una dintre axe, se obţine din figura de mai jos o ecuaţie pentru a determina presiunea maximă pe teren şi lungimea L' efectivă a fundaţiei, unde este evident că aria de bază nu este reactivă pentru o lungime egală cu L - L'.
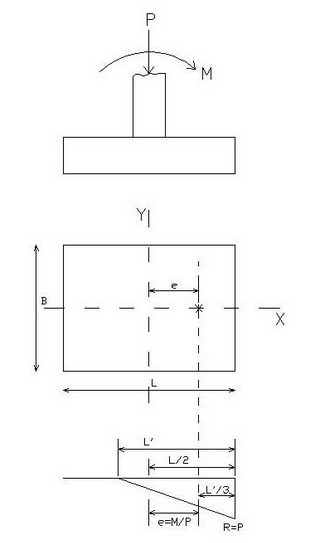
Aria triunghiului presiunilor trebuie să fie egală cu sarcina verticală P iar rezultanta trebuie să fie aplicată la L'/3 din segmentul cel mai solicitat şi să devină baricentrul triunghiului. Acest punct se găseşte la o distanţă
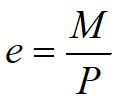
de la centrul fundaţiei astfel încât
![]()
şi
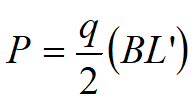
Înlocuind L' în expresia lui P şi rezolvând q se obţine
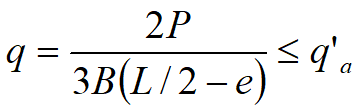
Cu p, q'a şi excentricitatea fixate, se rezolvă pentru B şi L prin încercări până la satisfacerea egalităţii.
Când este prezent momentul fie faţă de axa x sau de axa y, poziţia rezultantei este redată în figura de mai jos:
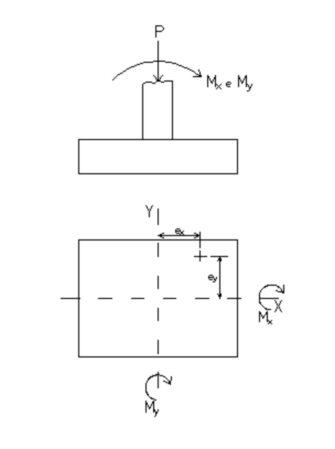
iar dacă ambele excentricităţi sunt:
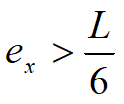
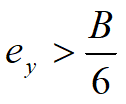
doar o parte a fundaţiei rezultă reactivă.
Presiunea pe teren, pentru fundaţii cu excentricitate faţă de ambele axe, poate fi calculată, când nu există nicio ridicare a fundaţiei faţă de teren, după cum urmează:
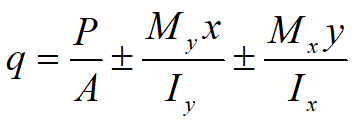
sau

Reamintim că
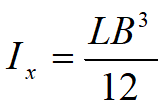
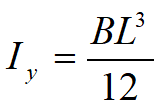
My este momentul faţă de axa y;
Mx este momentul faţă de axa x;
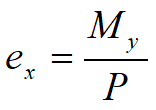
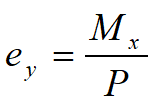
Direcţiile pozitive sunt cele ilustrate.
© GeoStru