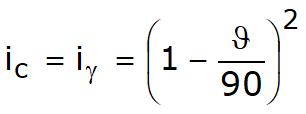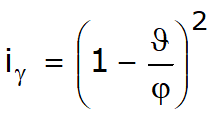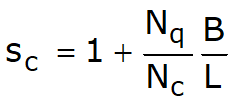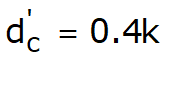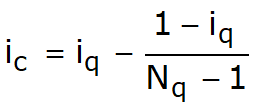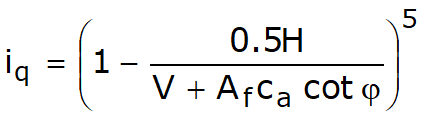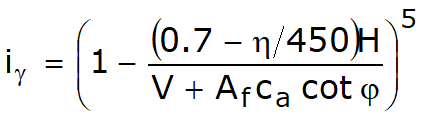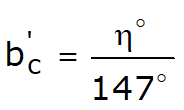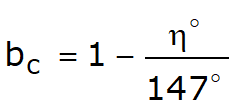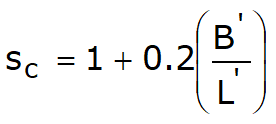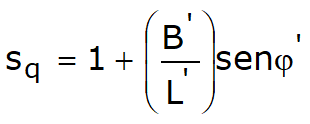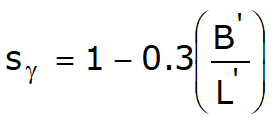<< Click to Display Table of Contents >> Navigation:  Loadcap > Teoria de calcul > Capacitatea portantă

Sarcina limită a unei fundații de suprafață poate fi definită în funcție de valoarea maximă de încărcare pentru care în niciun punct al subsolului nu se ajunge la condiția de rupere (metoda lui Frolich), sau în funcție de valoarea sarcinii, mai mare decât precedenta, pentru care fenomenul de ruptură dacă este extins la un volum mare al solului (metoda lui Prandtl și următorii).

Prandtl a studiat problema de ruptură a unui semispatiu elastic datorată efectului unei sarcini aplicate pe suprafata sa cu referire la oțel, caracterizând rezistență la forfecare cu o ecuație de tipul:

 

 

valida și pentru terenuri.

Ipotezele și condițiile introduse de Prandtl sunt:

•Material fără greutate și deci γ=0

•Comportament rigid-plastic

•Rezistența la forfecare estimabilă cu τ=c + σ´tg(φ)

•Sarcina uniformă, verticală aplicată pe o fâșie de lungimea infinită și de lățime 2b (stare de deformație plană)

•Tensiuni tangențiale nule la contactul dintre fâșia de sarcina și suprafață limita a semispatiului.

 

La forfecare se verifică și plasticizarea materialului dintre suprafețele limita ale semispatiului și suprafețele GFBCD.

În triunghiul AEB forfecarea se realizează în funcție de două familii de segmente rectilinii și înclinate la 45°+φ/2 față de orizontală.

În zonele ABF și EBC forfecarea se produce de-a lungul a două familii de linii, una constituită din segmente rectilinii care trec prin punctele A și E și o altă de arcuri din familia de spirale logaritmice.

Polii acestora sunt punctele A și E. În triunghiurile AFG și ECD ruptură se realizează pe segmente înclinate la ±(45°+ φ/2) în raport cu verticală.

 

 

 

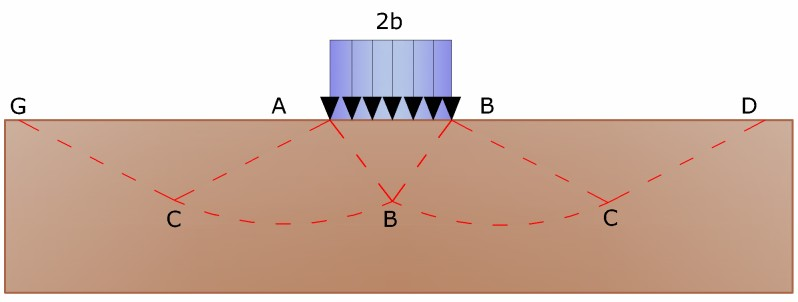
Identificând astfel volumul terenului adus la ruptura de sarcină limită, acesta poate fi calculat scriind condiția de echilibru dintre forțele agente pe orice volum de teren delimitat pe baza uneia dintre suprafețele de alunecare.

Se ajunge deci la o ecuație q =B × c, unde coeficientul B depinde numai de unghiul de frecare j al terenului.

 

 

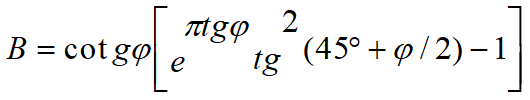
Pentru φ =0 coeficientul B este egal cu 5.14, deci q=5.14 × c.

In celalalt caz particular de teren necoeziv (c=0, g<>0) rezulta q= 0, dupa teoria lui Prandtl, nu ar fi posibil deci sa se aplice nicio sarcina pe suprafata limita a unui teren necoeziv.

De la aceasta teorie, chiar daca nu se aplica practic, au luat nastere cercetarile si metodele de calcul urmatoare.

De fapt  Caquot s-a pus in aceleasi conditii ca si Prandtl exceptie facand faptul ca fasia de sarcina nu mai este aplicata pe suprafata semispatiului, dar la o adancime h, cu h<2b; terenul dintre suprafata si adancimea h are urmatoarele caracteristici: g<>0, φ=0, c=0

si este deci un mediu care are greutate dar nu are rezistenta.

 
Rezolvand ecuatiile echilibrului se ajunge la expresia:

 

 

 

care, in mod sigur este un pas inainte fata de Prandtl, dar care inca nu oglindeste realitatea.

 

 

 

Metoda lui Terzaghi (1955)

 

Terzaghi , urmand studiul lui Caquot, a adus anumite modificari pentru a tine cont de caracteristicile efective ale cuplului lucrare de fundatie - teren.

Sub actiunea sarcinii transmisa de fundatie terenul care se gaseste in contact cu fundatia are tendinta de al aluneca lateral, dar este impiedicat de catre rezistentele tangentiale care se dezvolta intre fundatie si teren. Aceasta aduce cu sine o modificare a starii de tensiune in terenul de sub fundatie; pentru a tine seama de aceasta Terzaghi asigneaza laturilor AB si EB ale marginii lui Prandtl o inclinatie y  fata de orizontala, alegand valoarea lui y in functie de caracteristicile mecanice ale terenului la contactul teren- fundatie.

Ipoteza γ2 =0 pentru terenul de sub fundatie este depasita admitand ca suprafetele de ruptura raman nealterate, expresia sarcinii limita este deci:

 

 

in care c este un coeficient care rezulta in functie de unghiul de frecare φ al terenului de sub suprafata de fundare si de unghiul φ definit anterior;

b este semi-latimea fasiei.

Mai mult, bazandu-se pe date experimentale, Terzaghi trece de la problema plana la problema spatiala introducand factori de forma.

O contributie ulterioara afost adusa de Terzaghi asupra comportamentului efectiv al terenului.

In metoda lui Prandtl se presupune un comportament rigid-plastic al terenului, Terzaghi in schimb admite acest comportament in terenurile foarte compacte.

In aceste terenuri, curba sarcini-tasari prezinta o prima un parcurs rectiliniu, urmat de un parcurs scurt curbiliniu (comportament elastico-plastic); ruptura este instantanee si valoarea sarcinii limita este clar identificata (ruptura generala).

Intr-un tren foarte afanat in schimb, relatia sarcini-tasari prezinta un parcurs curbiliniu accentuat incepand de la sarcinile cele mai usoare cu un efect de ruptura progresiva a terenului (ruptura locala); in concluzie aflarea sarcinii limita nu este atat de clara si evidenta ca si in cazul terenurilor compacte.

Pentru terenurile foarte afanate, Terzaghi propune sa se ia in considerare sarcina limita, valoarea care se calculeaza cu formula precedenta introducand totusi valorile reduse ale caracteristicilor mecanice ale terenului si anume:

 

 

Explicând coeficientii formului precedente, formula lui Terzaghi poate fi scrisa:

 

 

unde:

 

 

 

 

 

 

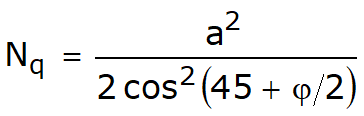
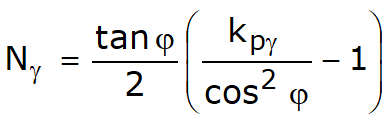
Formula lui Meyerhof (1963)

 

Meyerhof a propus o formula pentru calcularea sarcinii limita similara celei a lui Terzaghi; diferentele constau in introducerea unor coeficienti de forma ulteriori.

Acesta a introsus un coeficient sq care multiplica factorul Nq, factorii de adancime di si inclinatie ii pentru cazul in care sarcina transmisa fundatiei este inclinata pe verticala.

Valorile coeficientilor N au fost obtinuti de la Meyerhof ipotezand diferite arcuri de proba BF (v. mecanismul Prandtl) , in timp ce taierea de-a lungul planelor AF avea valori aproximate.

Factorii de forma aflati de catre Meyerhof sunt prezentati mai jos impreuna cu formula.

 

 

 

 

 

 

 

 

 

factor de forma:

 

 

 

 

 

factor de adâncime:

 

 

 

 

inclinatie:

 

 

 

unde :

 

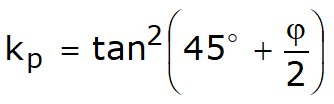
θ = Inclinatia rezultantei pe verticala.

 

 

 

Formula lui Hansen (1970)

 

Este o exensie ulterioara a teoriei lui Meyerhof; extensiile constau in introducerea lui bi care tin cont de o eventuala inclinatie pe orizontala a suprafetei de fundare si un factor gi pentru terenul inclinat.

Formula lui Hansen este valabila pentru orice raport D/B, deci atat pentru fundatii superficiale cat si pentru cele de adancime, dar acelasi autor a introdus coeficientii pentru o interpretare mai buna a comportamentului real al fundatiei, fara de care ar fi crescut prea mult sarcina limita cu adancimea.

 

 

Pentru valori  D/B <1

 

 

 

Pentru valori D/B>1:

 

 

 

In cazul  φ = 0

 

 

------------------------------------------------------------------------------------------------------------------------

   D/B      0           1            1.1            2            5            10            20            100

------------------------------------------------------------------------------------------------------------------------

 d'c        0           0.40          0.33         0.44        0.55        0.59           0.61        0.62

------------------------------------------------------------------------------------------------------------------------.

 

 

In factorii urmatori expresiile cu (') sunt valabile cand φ=0.

Factor de forma:

 

 

 

Factor de adâncime:

 

 

Factori de inclinatie a sarcinii:

 

 

 

 

Factori de inclinatie a terenului (fundatie pe versant):

 

 

 

Factori de inclinatie a planului de fundare (baza inclinata)

 

 

 

 

Formula lui Vesic (1975)

 

Formula lui Vesic este analoaga formulei lui Hansen, cu Nq si Nc ca pentru formula lui Meyerhof si Nγ ca mai jos:

 

 

Factorii de forma si de adancime care apar in formulele de calcul a capacitatii portante sunt la fel cu cei propusi de Hansen; cateva diferente se inregistreaza in factorii de inclinatie a sarcinii, a terenului (fundatie sau versant) si a planului de fundare (baza inclinata).

 

Formula Brich-Hansen (EC 7 - EC 8)

 

Atat timp cat o fundatie poate rezista, sarcina de proiect cu masuri de siguranta in ceea ce priveste ruptura generala, pentru toate combinatiile de sarcina face referire la SLU (starea limita ultima), trebuie sa fie satisfacuta urmatoarea inegalitate:

 

 

Unde Vd este sarcina de proiect la SLU, normala la baza fundatiei, cuprinzand si greutatea fundatiei; in timp ce Rd este sarcina limita a proiectului fundatiei in relatie cu sarcinile normale, tinand cont si de efectul sarcinilor inclinate sau excentrice.
In calcularea analitica a sarcinii limita a proiectului Rd trebuiesc luate in considerare situatiile pe termen scurt si lung in terenurile cu granulatie mica.

Sarcina limita in conditii nedrenate se calculeaza ca:

 

 

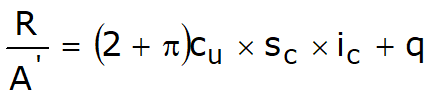
unde:

 

 

 

Pentru conditiile drenate sarcina limita de proiect este calculata dupa cum urmeaza:

 

 

Unde:

 

Factorii de forma

 

 

 

 

 Factori inclinatie rezultata datorata unei sarcini orizontale H paralela cu L’

 

 

 

 

 

 

Factori inclinatie rezultata datorata unei sarcini orizontale H paralela cu B’

 

 

 

 

In afara de factorii corectivi de mai sus sunt considerati aceia complementari adancimii planului de fundare si inclinatiei planului de fundare si a nivelului terenului. (Hansen).

 

 

Meyerhof e Hanna (1978)

 

Toate analizele teoretice studiate până acum sunt bazate pe presupunerea că subsolul este izotropic și omogen la o adâncime considerabilă. În natură, solul este în general neomogen cu amestecuri de nisip, argilă și prafuri în diferite proporții. În analiză este considerat în mod normal un profil mediu al terenului. Totuși, dacă solul are strate diferite cu diferite compoziții și caracteristici ale rezistențelor, presupunerea de omogenitate nu este validă atât timp cât suprafața de cedare intersectează acest tip de strate.

Prezenta analiză este limitată la un sistem cu două strate. Pentru o fundație localizată în stratul superior la o adâncime D, sub nivelul terenului, suprafața de cedare la sarcină ultimă se poate localiza fie integral în stratul superior sau poate trece granița dintre cele două strate. Mai mult, este posibil ca stratul superior să aibă o rezistența mare și cel inferior o rezistență mică sau invers. În oricare caz, o analiză generală pentru (c = 0) va fi prezentată și va demonstra că aceeași analiză este corectă dacă stratele sunt compuse din nisip sau argilă.

Capacitatea portantă a sistemului de strate a fost analizată pentru prima dată de Button (1953) care a considerat doar argila saturată (j = 0). Mai târziu Brown și Meyerhof (1969) au arătat că analiza lui Button duce la rezultate nesigure.

Vesic (1975) a analizat rezultatele lui Brown și Meyerhof și a dat o soluție proprie acestei probleme.

Vesic a considerat ambele tipuri de teren în fiecare strat, terenuri tip argilă și (c = 0). Totuși, confirmările validității analizei lui Vesic nu sunt disponibile. Meyerhof (1974) a analizat un sistem de două strate compuse din nisip dens pe argilă moale și nisip afânat pe argilă tare și și-a susținut analiza cu modele de test. Meyerhof și Hanna (1978) au avansat cu analiza lui Meyerhof (1974) pentru a cuprinde solul (c = 0) și au susținut analiza cu un model de test. Secțiunea curentă se referă la metodele Meyerhof (1974) și Meyerhof și Hanna (1978).

 

 

Cazul 1: Un strat cu o rezistență mai mare se află deasupra unui deposit cu rezistența scazută
 

Figura 12.16 (a) arată o talpă continua de lațime B la o adâncime D sub nivelul terenului într-un strat cu rezistență mare (Layer 1). Adâncimea până la graniță cu stratul mai slab rezistent (Layer 2) sub baza fundației este H. Dacă această adâncime H este insuficientă pentru a forma o zonă completă de cedare plastică în stratul 1 în condiții de sarcină ultimă, o parte a acestei sarcini ultime va fi transferată la nivelul graniței mn. Această sarcină va induce o condiție de cedare în stratul mai slab (Layer 2). Totuși, dacă adâncimea H este destul de mare, atunci suprafața de cedare va fi localizată complet în Layer 1 după cum se poate vedea în Fig. 12.16b.

 

 
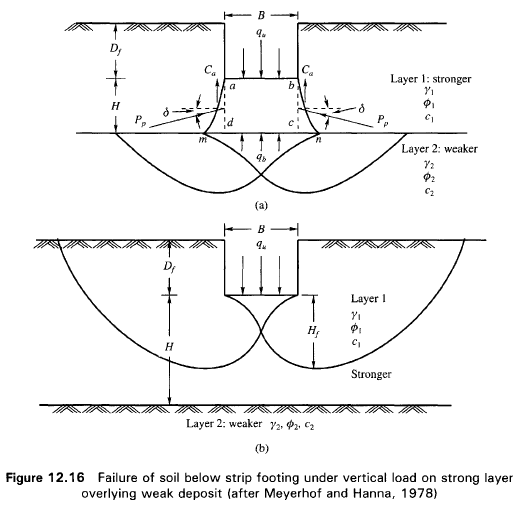
Capacitățile portante ultime ale tălpiilor continue la suprafața stratelor consistente și omogere Layer 1 și Layer 2 pot fi exprimate astfel:

Layer 1

Layer 2

Unde:

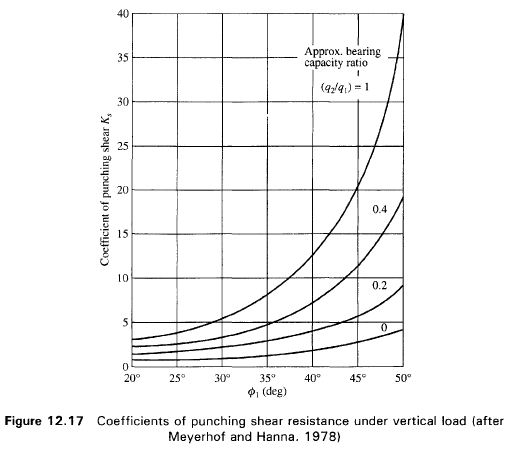
•Nc1, Nγ1= factorii de capacitate portantă pentru terenul din Layer 1 pentru unghiul de frecare φ1;

•Nc2, Nγ2= factorii de capacitate portantă pentru terenul din Layer 2 pentru unghiul de frecare φ2.

Pentru fundația aflată la adâncimea Df dacă suprafața de cedare se află în întregime în stratul Layer 1 (Fig. 12.16(b)) expresia pentru capacitatea portantă ultimă a stratului de suprafață poate fi exprimată ca:

 

 

 

Dacă q1 este mult mai mare decât q2 și dacă adâncimea H este insuficientă pentru a formă o conditie de cedare plastică totală în Layer 1, atunci cedarea fundației poate fi considerată datorată împingerii solului în graniță și trece de stratul de suprafață în stratul mai slab. Forțele ce acționează pe aceste suprafețe (pe unitate de lungime a fundației):  

 

 

 

Unde:

•qb= capacitatea portantă ultimă a Layer 2;

•Ca= forța de adeziune;

•Pp= presiune pasivă a terenului;

•δ= inclinația lui Pp față de normală.

 

 

 

 

 

 

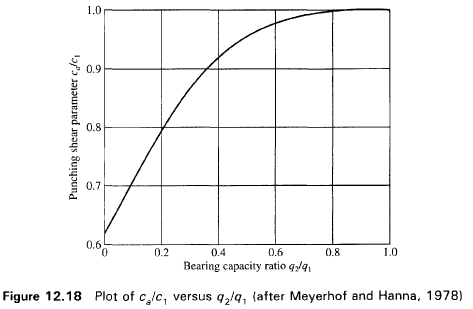
Richards et al.

 
Richards, Helm si Budhu (1993) au dezvoltat o procedura care permite, in conditii seismice, calcularea atat a sarcinii limita cat si a tasarilor induse, si deci calcularea ambelor stari limita (ultima si de deformatie). Calcularea sarcinii limita vine ca urmare a unei simple extensii a problemei sarcinii limita in cazul prezentei fortelor de inertie in terenul de fundare datorate seismului, in timp ce calcularea tasarilor se obtine prin abordarea lui Newmark (cfr. Apendice H din "Aspecte geotehnice ale proiectarii in zona seismica" - Asociatia Geotehnica Italiana). Autori au extins formula clasica trinomica a sarcinii limita:

 

 

Unde factorii de capacitate portanta sunt calculati cu urmatoarele formule:

 

 

Examinand cu o abordare de echilibru limita, un mecanism de tip Coulomb si luand in comsiderare fortele de inertie ce actioneaza pe volumul de teren la ruptura. In camp static, mecanismul clasic al lui Prandtl poate fi aproximat dupa cum se vede in figura de mai jos, eliminand zona de tranzitie (evantaiul lui Prandtl) redusa doar la linia AC, care este considerata ca un zid ideal in echilibru sub actiunea impingerii active si a impingerii pasive primite de la penele I si III:

 

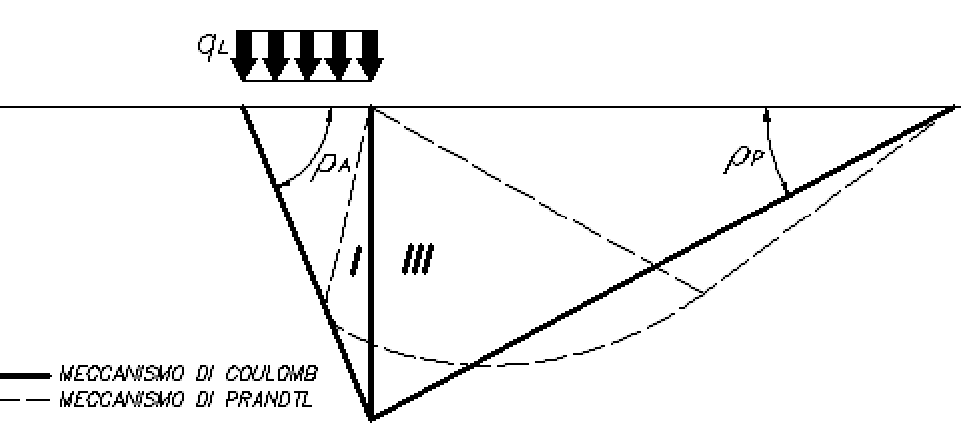
Schema de calcul a sarcinii limita (qL)

 

Autorii au obtinut expresiile unghiurilor ρA si ρP  ce definesc zonele de impingere activa si pasiva, precum si a coeficientilor de impingere activa si pasiva KA si KP in functie de unghiul de frecare intern φ al terenului si de unghiul de frecare δ teren - zid ideal:

 

 

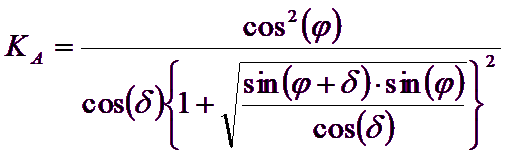
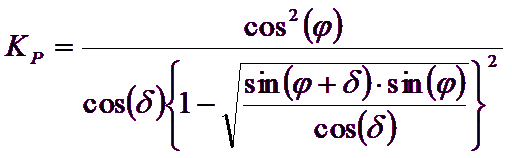
Trebuie oricum observat ca folosirea formulelor precedente luand φ=0.5δ , duce la valori ale coeficientilor de sarcina limita foarte apropiati celor bazati pe analiza de tip Prandtl. Richards et. al. au extins deci aplicarea mecanismului lui Coulomb la cazul seismic, tinand cont de fortele de inertie ce actioneaza pe volumul de teren la rupere. Aceste forte de masa, datorate acceleratiilor kh γ si kv γ , ce actioneaza in directie orizontala si verticala, sunt la randul lor egale cu kh γ si kv γ. Au fost obtinute astfel extensiile expresiilor lui ρa si ρp, precum si KA si KP, respectiv indicate ca ρAE si ρPE  si ca KAE si KPE pentru denotarea conditiilor seismice.

 

 

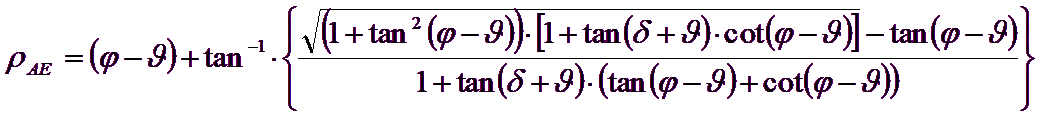
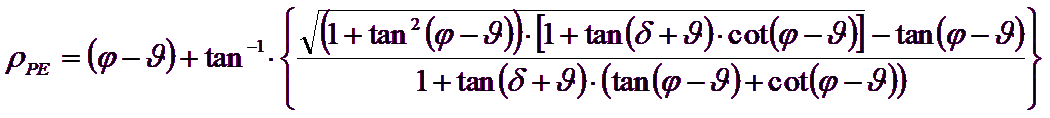
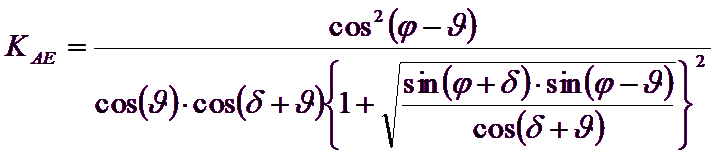
Valorile lui Nq si Nγ sunt determinabile folosind formulele precedente, implicand expresiile unghiurilor ρAE si ρPE si a coeficientilor KAE si KPE relative cazului seismic. In aceste expresii apare unghiul θ definit ca:

 

 

În tabela de mai jos sunt factorii de capacitate portanta calculati pentru urmatoarele valori ale parametrilor:

 

φ = 30°
δ = 15°

 

Si pentru diverse valori ale coeficientilor de impingere seismica:

Tabelul factorilor de capacitate portanta pentru φ=30°

 

 

 

 

 

 

 

© GeoStru