Cunoscându-se acţiunea exterioară pe radier,
{F}T=(Fx , Fy , Fz , Mx, My, Mz)
(fig.B.1) se cere:
-determinarea deplasărilor {DT}T=(u, v, w, θx, θy, θz);
-determinarea eforturilor {fi}T=(fx, fy, fz, mx, my, mz) în secţiunea de încastrare a fiecărui pilot i, în radier;
-determinarea diagramelor de eforturi secţionale în lungul fiecărui pilot;
-verificarea de rezistenţă a secţiunii piloţilor şi verificarea la capacitatea portantă în raport cu terenul;
-verificarea, dacă este cazul, la starea limită de deformaţii.
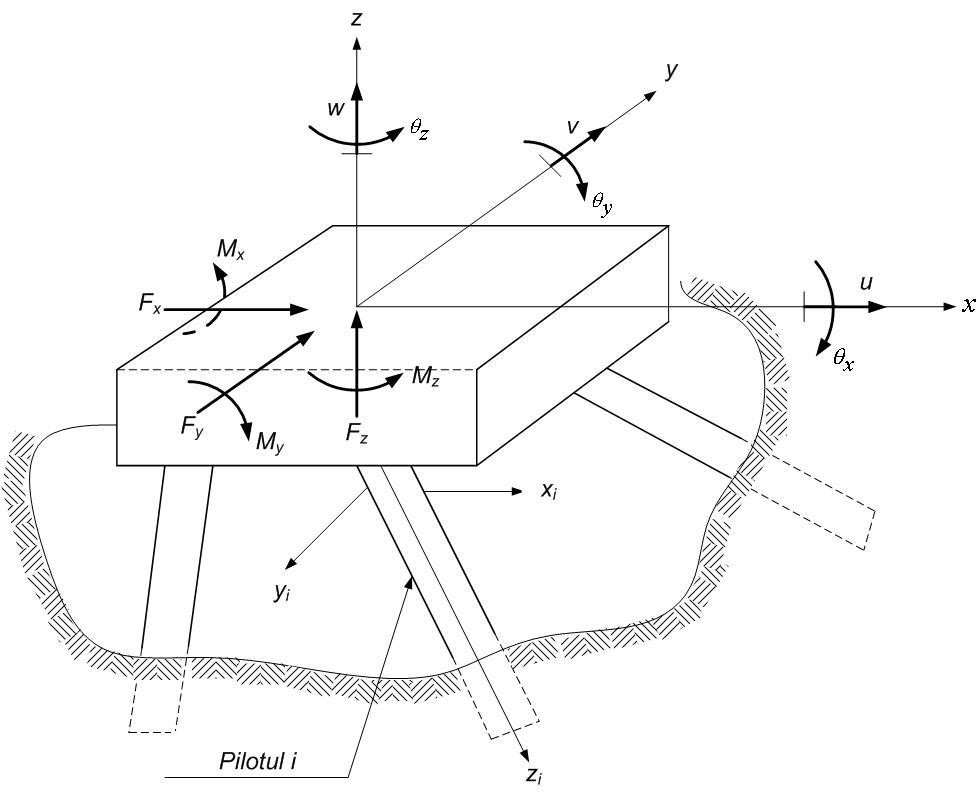
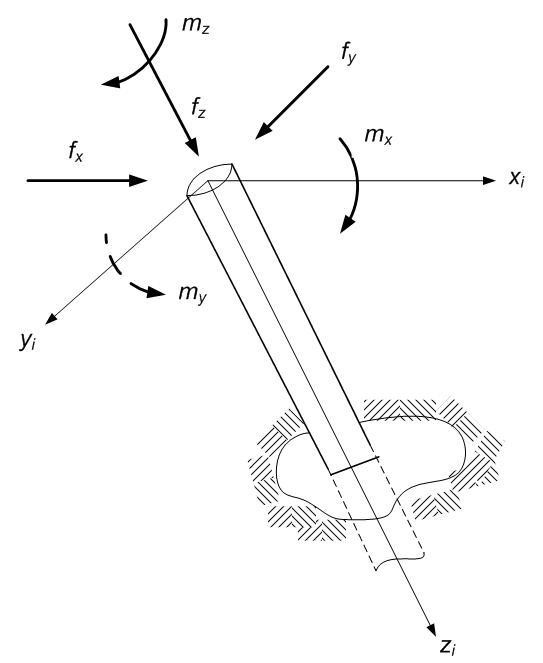
Fig. B.1
Calculul se efectuează în următoarele etape:
-se determină matricea de rigiditate [Ki] a fiecărui pilot i, în raport cu sistemul local de axe Oixiyizi , conform pct. B.3;
-se determină matricea de rigiditate a grupului de piloţi [K] în raport cu sistemul general de axe, Oxyz, prin asamblarea rigidităţilor locale şi transformarea sistemelor de coordonate;
-se rezolvă sistemul de ecuaţii: [K}{D}={F} şi se determină vectorul deplasărilor radierului, {D};
-se determină vectorul deplasărilor {di} la capul fiecărui pilot, în raport cu sistemul propriu de axe: {di}=[ri][li]{D}
-în care [ri][li] sunt matricele de transformare a axelor prin rotaţie şi respectiv translaţie;
-se determină solicitările pe capul pilotului: {fi}=[Ki]{di}
-se efectuează calculul eforturilor în lungul axei pilotului, conform prevederilor din anexa A;
-se fac verificări de rezistenţă ale secţiunii pilotului conform reglementărilor tehnice specifice;
-se fac verificări la capacitatea portantă în raport cu terenul conform pct. 5.2;
-se fac verificări la starea limită de deformaţii, dacă se impun.
Determinarea flexibilităţii pilotului izolat
Se consideră un pilot izolat definit în sistemul local de axe (fig. B.2). Se aplică, în mod succesiv, câte o solicitare unitară fx=1, fy=1, fz=1, mx=1, my=1 şi mz=1 în capul pilotului, şi se determină conform prevederilor din anexa A, deplasările δxx, δyy, δxθ = δθx, δyθ = δθy, δθθx, şi δθθy, mărimi ce au semnificaţia de coeficienţi de flexibilitate.
OBSERVAŢII:
1.În cazul piloţilor cu simetrie axială a secţiunii transversale:
δ xx = δ yy = δ x
δθθx = δθθy = δθ
δ xθ = δ yθ = δθx = δθy
2.În cazul piloţilor cu fişă liberă l0, expresiile coeficienţilor de flexibilitate se determină adăugând la deplasările calculate la nivelul terenului, deplasările pe consola de lungime l0, astfel:
![]()
![]()
![]()
Pentru gradele de libertate necuplate de translaţia axială, deplasarea δz şi răsucirea δφ se determină astfel:
a)La translaţie verticală
-din încărcări de probă:
δz = s0 N0 |
|
unde: |
|
s0 |
deplasarea capului pilotului |
N0 |
încărcarea axială ce revine piloţilor din grup sub acţiuni permanente |
-pe baza unor modele teoretice adecvate.
OBSERVAŢII
1.În cazul piloţilor cu fişă liberă pe lungimea l0 trebuie să se ţină seama şi de efectele acesteia.
2.În cazul grupului de piloţi la care eforturile axiale pot varia foarte mult se recomandă folosirea flexibilităţii
diferenţiate pentru piloţii comprimaţi şi pentru cei supuşi la tracţiune.
b)La răsucire
-pe baza unor modele teoretice adecvate.
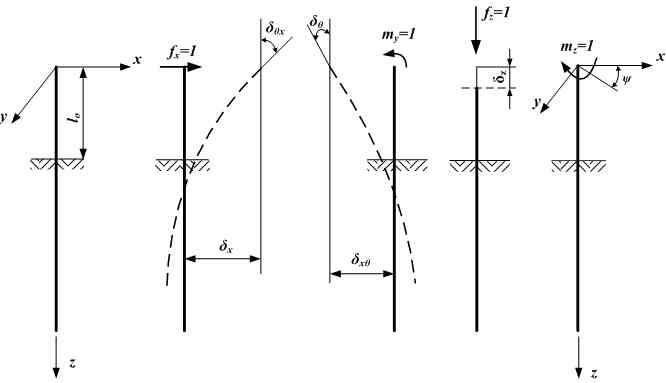
Fig. B.2
Determinarea matricii de rigiditate [Ki] a pilotului izolat. Matricea de rigiditate are forma:
|
u |
v |
w |
θx |
θy |
θz |
fx |
Kx |
0 |
0 |
0 |
Kθ |
0 |
fy |
0 |
Ky |
0 |
Kyθ |
0 |
0 |
fz |
0 |
0 |
Kz |
0 |
0 |
0 |
mx |
0 |
Kθy |
0 |
Kθ(x) |
0 |
0 |
my |
Kθx |
0 |
0 |
0 |
Kθ(y) |
0 |
mz |
0 |
0 |
0 |
0 |
0 |
Kφ |
unde:
![]()
![]()
![]()
K z = 1/ δz
K φ = 1/ δφ
OBSERVAŢIE
Indicii din paranteze arată că relaţia se aplică şi pe direcţia (y).
În cazul piloţilor având secţiunea transversală cu simetrie axială mărimile după cele 2 direcţii din plan sunt egale.
În cazul grupului plan de piloţi (fig. B.3) sistemul (B.1) devine:
K xx u + K xz w + K xθ θy = Fx
K zx u + K zz w + K zθ θy = Fz
K θx u + K θz w + K θθ θy = M y
unde:
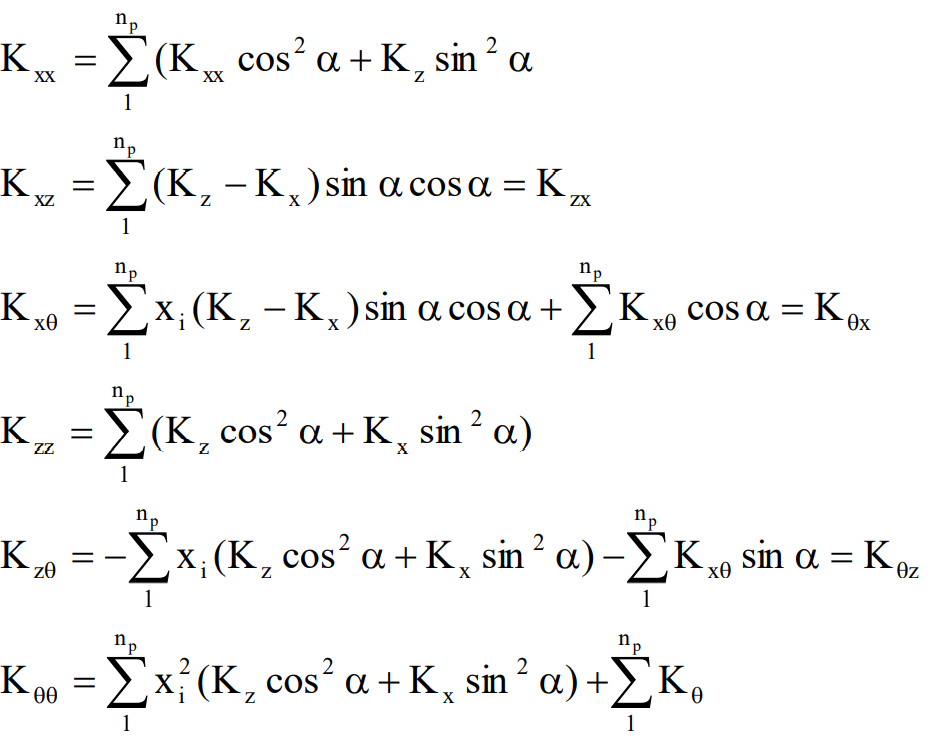
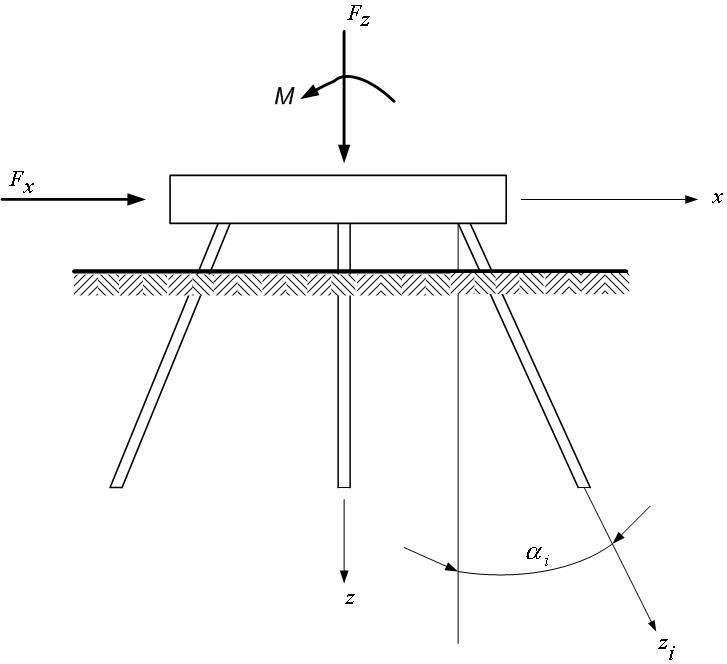
Fig B.3
© GeoStru