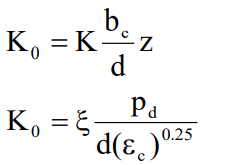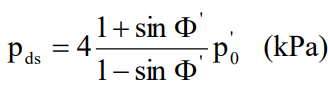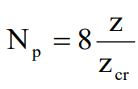1.1 NP 123-2022 > C. Determinarea valorilor unor parametri geotehnici necesari pentru calculul piloților în conlucrarea cu terenul

Valorile parametrilor geotehnici utilizaţi în calculul piloţilor se recomandă să fie determinate experimental.

În lipsa unor date experimentale complete pot fi utilizate valorile precizate în prezenta anexă, cu condiţia verificării piloţilor prin încărcări de probă.

Determinarea coeficientului reacţiunii laterale, Es, variabil linear cu adâncimea, z. Coeficientul Es se determină cu relaţia:

Es = Kbc z (kPa)
unde:
z	adâncimea punctului de calcul față de cota terenului natural
K	coeficient de proporţionalitate, în kilonewtoni pe metru la puterea a patra, conform tabelului C.1; coeficientul K se determină pentru straturile de pământ aflate până la o adâncime lk , în metri, care se calculează cu relaţia: lk = 3l0 ≤ D
unde:
	l0	conform tabel 15
	D	fişa pilotului sau baretei, în metri
bc	lăţimea de calcul, în metri, se determină astfel: 1. Pentru piloţi bc = d (1+tgf’med)
	2. Pentru barete, când încărcarea laterală se aplică perpendicular pe latura cea mai mare a secţiunii transversale, l bc = l+2b tgf’med
unde:
	d	diametrul pilotului, în metri
sau
	b	latura mică a secţiunii transversale a baretei, paralelă cu direcţia planului de acţiune a încărcării laterale, în metri
	f’med	valoarea caracteristică a unghiului de frecare internă în termeni de eforturi efective; valoarea f’med se calculează ca medie ponderată (prin tgf’) pentru straturile de pământ aflate până la adâncimea lk
3. Pentru barete, când încărcarea laterală se aplică perpendicular pe latura cea mai mică a secţiunii transversale, b, se utilizează graficele din figura C.1; pentru valori intermediare se interpolează liniar; valorile f’ din grafice sunt valori medii, f’med, calculate ca medie ponderată (prin tgf’) pentru straturile de pământ aflate până la adâncimea lk
Se verifică condiţia:

1. bc – d ≤ t (piloţi, cazul 1)
2. bc – l ≤ t (barete, cazul 2)
3. bc – b ≤ t (barete, cazul 3)
unde:
t	distanţa liberă minimă (lumina) dintre 2 elemente (piloţi sau barete) vecine, corespunzatoare direcţiei pe care s-a calculat bc, în metri

OBSERVATIE

Dacă în limitele grosimii lk se întâlnesc mai multe straturi caracterizate prin coeficienţi de proporţionalitate Ki diferiţi (cu peste 50%) faţă de media ponderată linear cu grosimile, iar grosimea fiecărui strat hi este cel puţin egală cu lăţimea

de calcul a pilotului bc , se evaluează un coeficient echivalent, K , cu relaţia:

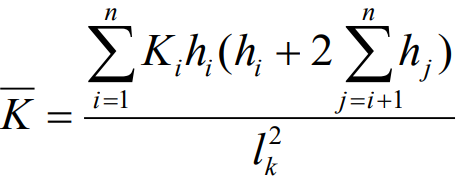
clip0047

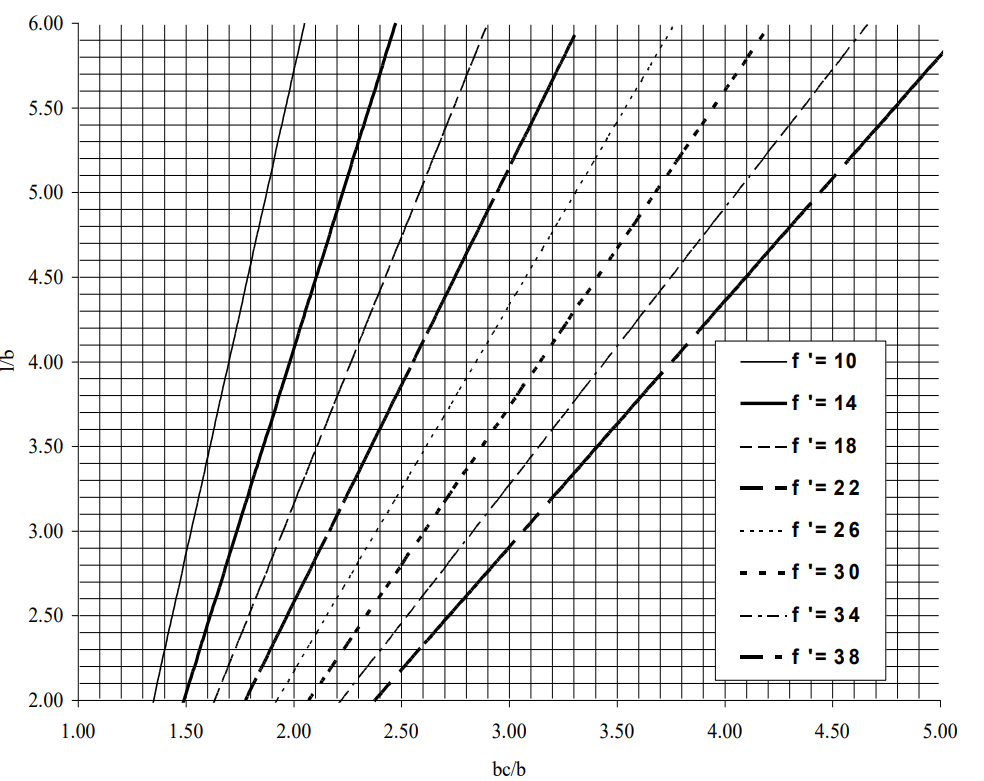
clip0048

Fig. C.1

Construirea curbelor p-y în ipoteza terenului nelinear

Curba p-y la o cotă curentă z, (fig. C.2) se compune, de regulă, din următoarele porţiuni:

- Porţiunea OA, ce se determină cu relaţia:

		valabilă pentru p ≤ pd şi y ≤ βd
unde:
pd	presiunea ultimă de calcul determinată conform pct. C.3.2 sau C.3.3 în kilonewtoni pe metru pătrat
α	coeficient de siguranţă, determinat cu relaţia:

β	coeficient ce depinde de tipul pământului şi al încărcării, care se ia : b=0.04 pentru pământuri necoezive şi conform tabelului C.2 pentru pământuri coezive;
K0	panta iniţială care se ia astfel:
		la pământuri necoezive la pământuri coezive
ξ	coeficient conform tabelului C.2
εc	deformaţia axială determinată prin încercarea la compresiune triaxială, corespunzătoare la 50 % din deviatorul de rupere; în lipsa datelor experimentale se pot adopta valorile precizate în cadrul observaţiei de sub tabelul C.2.

Tabelul C.1

Tipul pământului	Coeficientul de proporţionalitate K, kN/m4
Tipul pământului	piloţi prefabricaţi	piloţi executaţi pe loc
Argile şi argile prăfoase având Ic ≤ 0.25	650…2500	500…2000
Argile şi argile prăfoase având 0.25 < Ic ≤0.5; Prafuri nisipoase având Ic ≤ 1.00; Nisipuri prăfoase având 0.6 ≤ e <0.8	2500…5000	2000…4000
Argile şi argile prăfoase având 0.5 < Ic ≤1.00; Prafuri nisipoase având Ic >1.00 ; Nisipuri fine şi nisipuri mijlocii	5000…8000	4000…6000
Argile şi argile prăfoase având Ic >1.00; Nisipuri mari	8000…13000	6000…10000
Nisipuri cu pietriş, pietrişuri şi bolovănişuri cu umplutură de nisip.	-	10000…20000

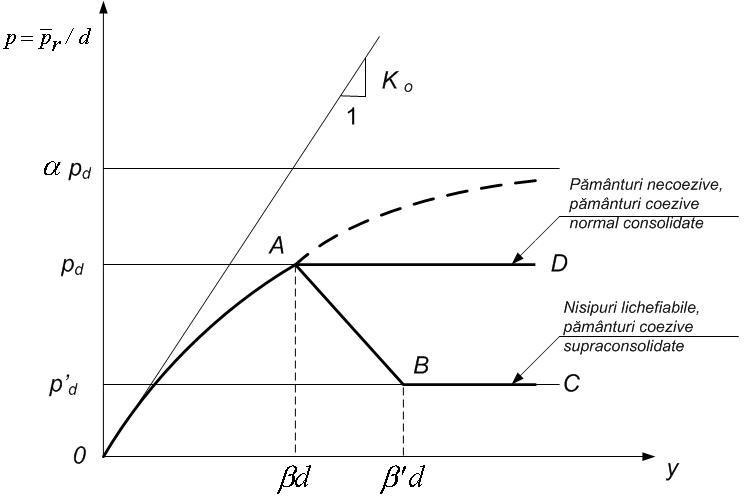
clip0046

Fig. C.2

Porţiunea AB, liniară, caracteristică pământurilor ce pot suferi degradări structurale la diferite tipuri de solicitări (argile supraconsolidate, nisipuri afânate saturate solicitate ciclic etc.).

Presiunea pd reprezintă rezistenţa reziduală şi se determină prin încercări de laborator.

În mod aproximativ, pentru argile se poate aprecia deplasarea necesară mobilizării rezistenţei reziduale cu relaţia:

y = β’d
unde:
β’	conform tabelului C.2.

Porţiunea liniară orizontală, după caz, AD sau BC.

Tabelul C.2

Parametrul	Tipul încărcării	Tipul pământului coeziv
Parametrul	Tipul încărcării	Normal consolidat	Supraconsolidat
ξ β β’	Statică	10 20εc 80εc	30 5εc 8εc
ξ β β’	Ciclică	10 7.5εc 20εc	30 2.5εc 5εc

OBSERVAŢIE

În lipsa datelor experimentale, pentru analize preliminare, se pot adopta următoarele valori pentru deformaţia axială εc :

-argile având Ic < 0.5 εc = 0.02

-argile având 0.5 ≤ Ic <1.00 εc = 0.01

-argile având Ic > 1.00 εc = 0.005

Calculul presiunii ultime pentru pământuri coezive

Cazul acţiunii statice


unde:
Φ’	unghiul de frecare interioară efectivă, în grade
p’	presiunea verticală efectivă la cota z, în kilopascali

Cazul acțiunii ciclice

pentru adâncimi z ≤ 2d

şi

pentru adâncimi z > 2d

Calculul presiunii ultime pentru pământuri coezive

pd = N p cu
unde:
cu	coeziunea aparentă nedrenată, de calcul;
Np	coeficient care variază linear cu adâncimea; se determină astfel:
		- în cazul solicitărilor statice
		- în cazul solicitărilor ciclice
zcr=10d		la pământuri normal consolidate sau uşor supraconsolidate
zcr=5d		la pământuri supraconsolidate