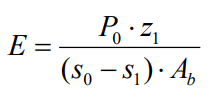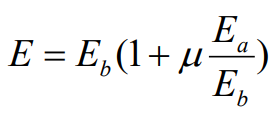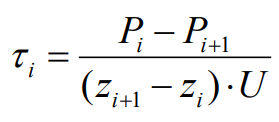<< Click to Display Table of Contents >> Navigation:  1.1 NP 123-2022 > Metodologia pentru determinarea prin încărcare de probă a transferului de încărcare axială cu ajutorul reperilor mecanici

Metodologia se foloseşte la piloţi sau barete. Exemplul prezentat se referă la o baretă instrumentată. În cazul în care între bareta solicitată axial şi teren au loc deplasări relative, rezistenţa la frecare pe suprafaţa laterală a baretei poate fi mobilizată. Procesul de transmitere prin frecare a încărcării axiale de la baretă la terenul înconjurător poartă numele de transfer de încărcare.

 

În vederea determinării transferului de încărcare este necesară cunoaşterea distribuţiei deformaţiei în adâncime în corpul baretei. În acest scop bareta se instrumentează cu reperi mecanici (fig.E.1) plasaţi la diferite cote de observaţie.

Un reper mecanic este alcătuit dintr-o tijă metalică sudată de o placă de bază. Tija este protejată faţă de betonul din corpul baretei printr-o ţeavă rezemată pe placa de bază prin intermediul unei garnituri de cauciuc. Pentru a evita frecarea între tijă-reper şi ţeava de protecţie, se prevăd din loc în loc distanţiere inelare din cauciuc. La capătul superior se prevede un capac de care tija-reper se solidarizează, înainte de începerea încărcării, printr-o piuliţă.

Reperii mecanici se solidarizează de carcasa de armătură a baretei, la interiorul acesteia şi sunt coborâţi odată cu carcasa în tranşeea forată, înainte de betonare. Prin betonare, plăcile de bază se înglobează în corpul baretei reprezentând reperi ai tasării baretei la cota la care au fost introduse. În figura E.2 se indică, într-o secţiune verticală prin baretă, schema de amplasare a reperilor mecanici.

Pentru obţinerea distribuţiei de deformaţii în adâncime, capetele tijelor-reper înglobate în baretă debuşează în ferestre practicate în corpul baretei (Detaliu A, fig. E.2). În acest scop, la pregătirea capului baretei (îndepărtarea, prin spargere, a stratului de beton din suprafaţă contaminat cu noroi şi turnarea în loc a unui beton corespunzător) se lasă cutii de cofraj pentru formarea ferestrelor.

De tija-reper se montează un microcomparator pentru înregistrarea deplasării relative între cota z şi cota capului baretei.

Important: Înainte de începerea determinării se va îndepărta piuliţa de fixare a capacului de protecţie a reperului.

 

Încărcarea de probă se efectuează cu respectarea SR EN 1997-1.

Citirile la reperii mecanici se înregistrează la fel ca la reperii care determină tasarea capului baretei.

 

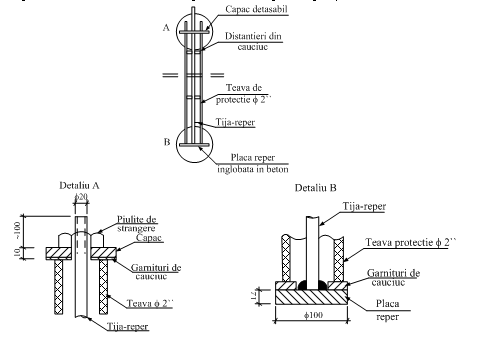
Fig. E.1

 

Prelucrarea rezultatelor

Deformaţiile în lungul corpului baretei

Pentru o anumită treaptă de încărcare, deformaţia si a corpului baretei la adâncimea zi la care este coborât reperul mecanic i se determină cu relaţia:

 

Deformaţiile si, înregistrate la diferite adâncimi pentru una şi aceeaşi treaptă de încărcare, se reprezintă la o scară convenabilă, raportându-se faţă de axul vertical al baretei. Se construieşte grafic sau analitic o curbă de variaţie cu adâncimea a deformaţiilor de compresiune în lungul baretei (fig.E.3.b).

 

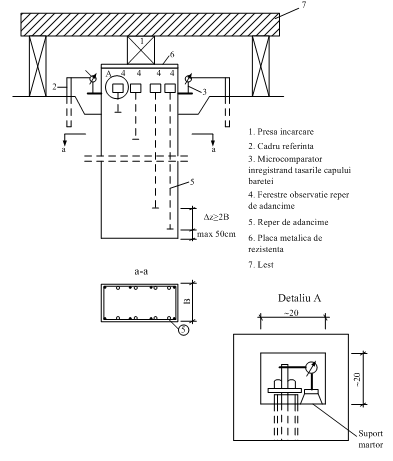
Fig. E.2

 

Deformaţiile specifice în lungul corpului baretei

Deformaţia specifică εi la cota zi se calculează cu relaţia:

 

Pe baza valorilor εi, calculate cu relaţia de mai sus, se construieşte curba de variaţie cu adâncimea a deformaţiei specifice (fig.E.3c).

 

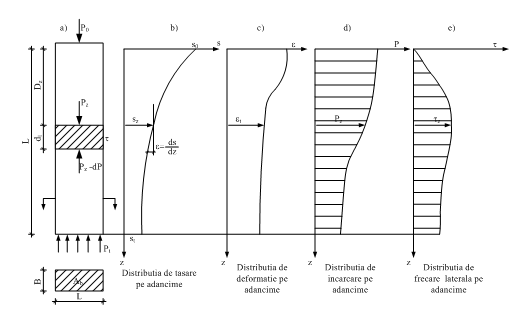
Fig. E.3

 

Forţa axială în lungul corpului baretei

Forţa axială Pi la adâncimea zi se calculează cu expresia:

 

 

Pe baza valorilor Pi calculate se construieşte curba de variaţie cu adâncimea a forţei axiale P (Fig. E.3.d).

 

OBSERVAȚIE

Este indicat ca cel mai scurt reper să fie plasat suficient de aproape de suprafaţa terenului, astfel să se poată practica, înainte de începerea încărcării, un şanţ de jur împrejurul baretei până la adâncimea acestui reper. În acest fel, pe zona cuprinsă între capul baretei şi cota primului reper, frecarea pe suprafaţa laterală lipseşte, iar încărcarea axială se transmite integral prin baretă.

 

Modulul de deformaţie al betonului din corpul baretei poate fi obţinut cu relaţia:

 

În lipsa valorilor E determinate experimental, modulul de deformaţie se va calcula cu relaţia:

 

Eb, Ea  se obţin din prescripţiile în vigoare pentru calculul elementelor de beton şi beton armat în funcţie de marca betonului şi tipul armăturii.

 

Efortul tangenţial mobilizat pe suprafaţa laterală

Efortul tangenţial τi mobilizat pe suprafaţa laterală a baretei la adâncimea zi se calculează cu expresia:

 

 

Pe baza valorilor τi calculate se construieşte graficul de variaţie cu adâncimea a efortului tangenţial mobilizat pe suprafaţa laterală (Fig E.3.e).

 

Determinare curbelor de transfer a încărcării

Într-un sistem de coordonate (s,τ) se reprezintă valorile deformaţiilor baretei, si, la o adâncime dată, zi, stabilite cu relaţia (E.1) în corelare cu valorile efortului tangenţial τi calculate cu relaţia (E.6), pentru diferite valori ale încărcării P0 aplicată la capătul baretei. Se obţine astfel o curbă care arată mărimea deformaţiei necesară a fi atinsă la adâncimea zi pentru a se mobiliza efortul tangenţial pe suprafaţa laterală a baretei, denumită curbă de transfer (fig.E.4).

Comparându-se  valoarea  maximă  a  lui  tmax   de  pe  curba  de  transfer  ( ab )  cu  valoarea rezistenţei la forfecare a pământurilor la aceeaşi adâncime, τ f,zi  obţinută prin încercări de laborator sau pe teren ( bc ) se obţin valorile coeficientului de reducere, λi.

 

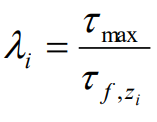
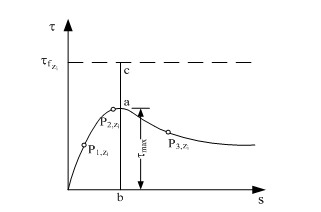
Fig. E.4

 

Determinarea diagramelor de variaţie a forţei axiale transmisă prin suprafaţa bazei, Pv şi  forţei axiale transmisă prin frecare pe suprafaţa laterală, Plat

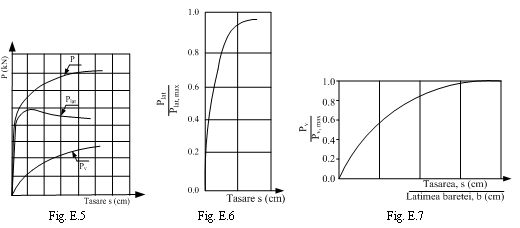
Forţa Pv la baza baretei corespunzătoare diferitelor trepte de încărcare P0 se calculează cu relaţia (E.3). Scăzând Pv  din P0  se obţine Plat care reprezintă cota-parte din forţa totală P0 preluată prin frecare pe suprafaţa laterală. În sistemul de coordonate (s,P) se construiesc curbele (s,P0), (s,Pv) şi (s,Plat), după cum arată în figura E.5.

 

Determinarea mărimii absolute a tasării baretei pentru care se produce mobilizarea integrală a frecării pe suprafaţa laterală

Pe baza valorilor Plat = f(s) din curba din figura E.5 se calculează rapoartele Plat / Plat,max. Valorile Plat / Plat,max  se reprezintă grafic în funcţie de tasările corespunzătoare, s (Fig. E.6).

 

Determinarea mărimii relative a tasării baretei pentru care se produce mobilizarea integrală a rezistenţei în planul bazei

Pe baza valorilor Pv = f(s) din curba din figura E.5 se calculează rapoartele Pv / Pv,max. Valorile Pv / Pv,max se reprezintă grafic în funcţie de tasările relative corespunzătoare, s/b, unde b este lăţimea baretei (Fig. E.7).

 

 

Exemplu de calcul

Se prezintă etapele de calcul pentru determinarea, prin încărcarea de probă a unei barete având dimensiunile în plan 2,60 x 0,80 m2 şi fişa de 7,50 m, instrumentată cu reperi mecanici, a transferului de încărcare. Treptele de încărcare aplicate pe bareta de probă, poziţia, lungimea şi numărul de ordine al reperilor ca şi citirile înregistrate la microcomparatoare sub fiecare treaptă de încărcare sunt prezentate în tabelul E.1.

 

Calculul deformaţiilor în lungul corpului baretei

Determinarea deformaţiilor si, sub treapta de încărcare P, se face cu relaţia:

si = s0 - Ci

 

Sub treapta de încărcare P0 = 3000kN, tasarea capului baretei, s0, a fost de 1,488 cm. Deformaţiile  în lungul corpului corpului baretei, sunt:

 

 

Deformaţiile în lungul corpului baretei, sub fiecare treaptă de încărcare, se determină în acelaşi mod. Valorile obţinute sunt date în tabelul E.2 (coloana 4).

 

Calculul și valorile deformaţiilor specifice în lungul corpului baretei sunt:

 

 

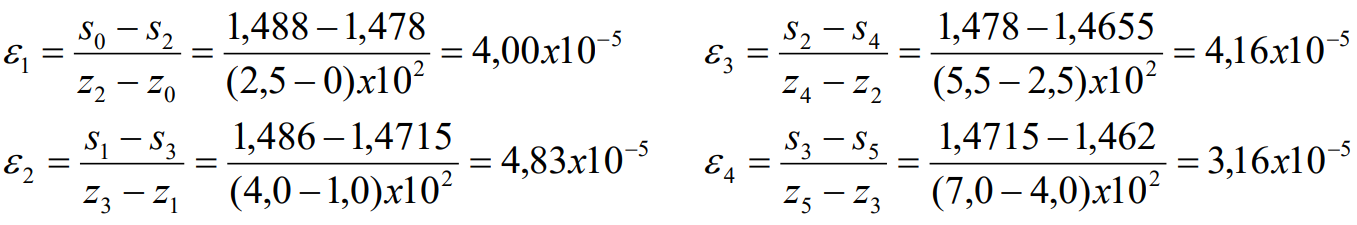
Deformaţia specifică ε5, nu se poate determina pentru că nu se cunoaşte s6 adică tasarea bazei baretei.

 

Observaţie:

Se constată că deformaţia specifică ε1, corespunzătoare părţii superioare din corpul baretei (cuprinsă între cotele 0,0 şi -2,5), este mai mică decât ε2 corespunzătoare zonei dintre cotele -1,0 şi 4,0. Este evident că acest lucru nu concordă cu situaţia reală, întrucât zona superioară a corpului baretei suferă deformaţia specifică maximă, fiind supusă la solicitarea maximă axială, pe această porţiune efectul transferului de încărcare fiind minim (neglijabil). Această inadvertenţă se constată sistematic la toate treptele de încărcare ceea ce conduce la ideea că, probabil, sunt erori în citirile înregistrate la microcomparatoarele pentru măsurarea tasării s0, deoarece deformaţia specifică aferentă zonei dintre cotele -1,0 şi -2,5m este:

 

Această valoare a deformaţiei specifice este în concordanţă cu celelalte valori corespunzătoare aceeaşi trepte de încărcare (P0 = 3000 kN) şi poate fi admisă ca fiind constantă pe porţiunea din corpul baretei cuprinsă între capul acesteia şi cota -2,5m.

 

Valorile εi pentru toate treptele de încărcare sunt înscrise în tabelul E.2 coloana 8.

 

Tabelul E.1

 

Tabelul E.2

 

 

Calculul forţei axiale în lungul corpului baretei

Valoarea modului de deformaţie, E, al betonului din corpul baretei corespunzătoare deformaţiei specifice ε1 = 5,3x10-5:

 

Valorile forţei axiale în lungul corpului baretei, sunt:

 

Valorile Pi, respectiv E corespunzătoare tuturor treptelor de încărcare sunt înregistrare în tabelul E.2, coloanele 5 şi 6.

 

Calculul efortului tangenţial mobilizat pe suprafaţa laterală

Efortul tangenţial, τi, mobilizat pe suprafaţa laterală. Valorile obţinute sunt:

 

 

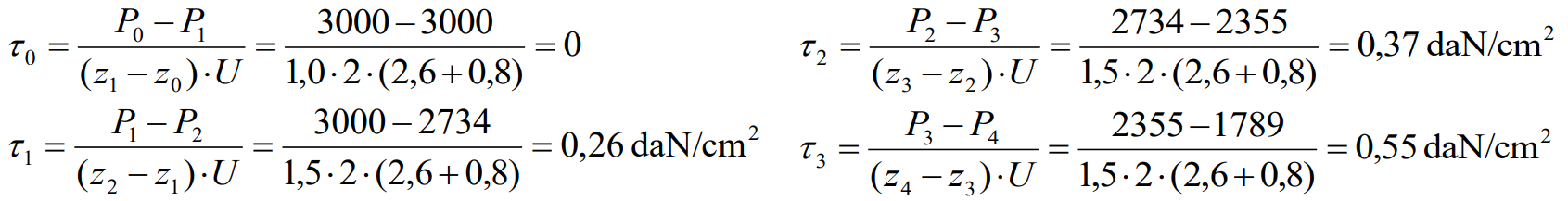
Valorile τi pentru toate treptele de încărcare sunt date în tabelul E.2. coloana 7.

Rezultatele  obţinute  prin  preluarea  datelor  înregistrate  în  timpul  încărcării  de  probă sunt prezentate sub formă grafică în figurile E.8 ÷ E.11.

 

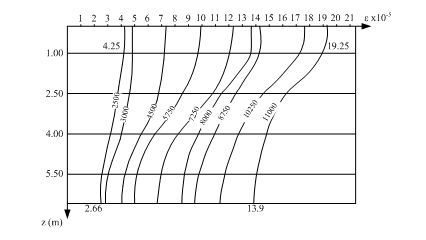
Fig. E.8

 

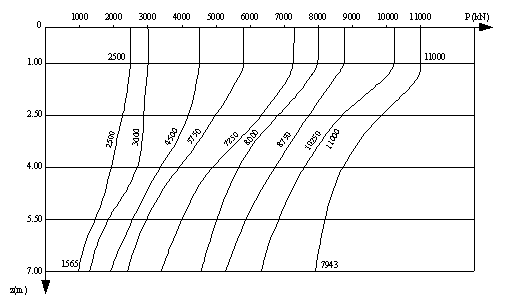
Fig. E.9

 

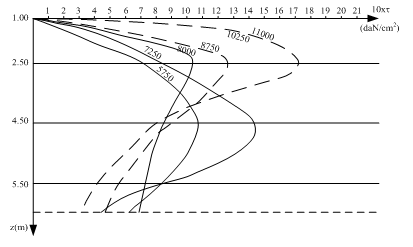
Fig. E.10

 

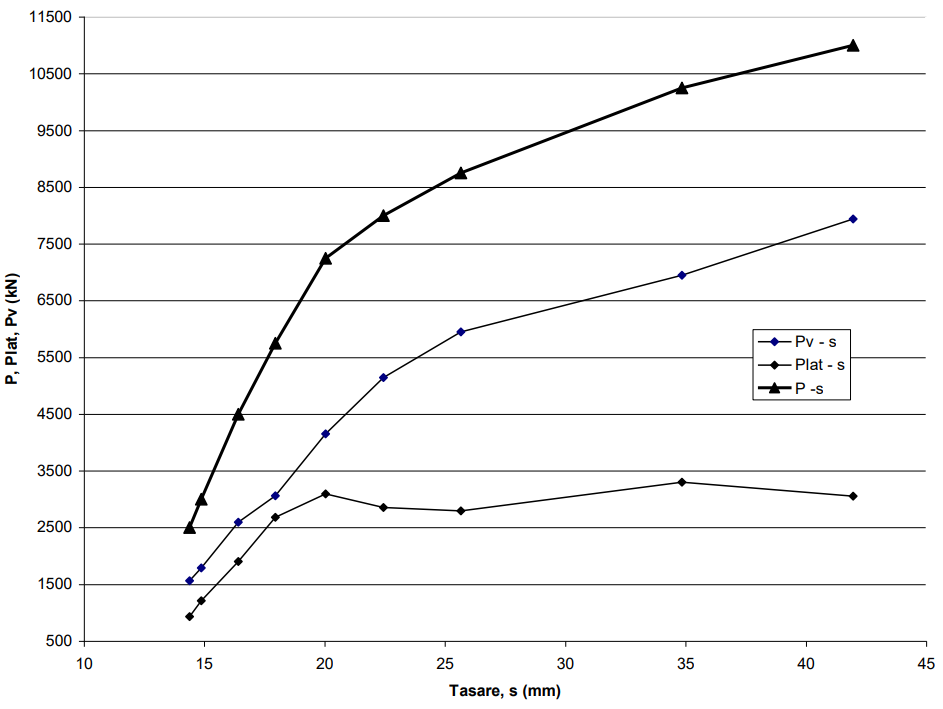
Fig. E. 11

 

 

 

© GeoStru