Forța de întindere în armătura „i” este dată de trei componente:
a)Forța de întindere datorată greutății proprii a umpluturii armate și suprasarcinii ce acționează la suprafața terenului, Ti1 (Figura 6.24).
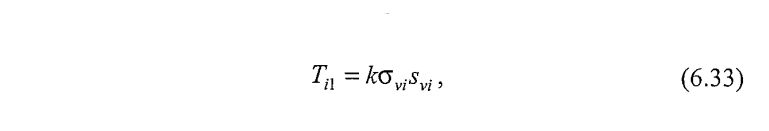
Unde:
k este coeficientul împingerii determinat conform 6.4.4.1,
σvi este presiunea la nivelul „i” conform distribuției Meyerhof,
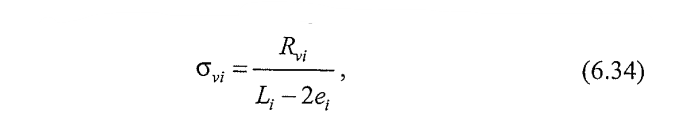
Unde:
Rvi este rezultanta forțelor verticale la nivelul armăturii „i”, afectată de factorii parțiali ai încărcărilor,
ei este excentricitatea rezultantei Rvi;
Svi este distanța pe verticală între armături la nivelul „i",
Li este lungimea armăturii „i".
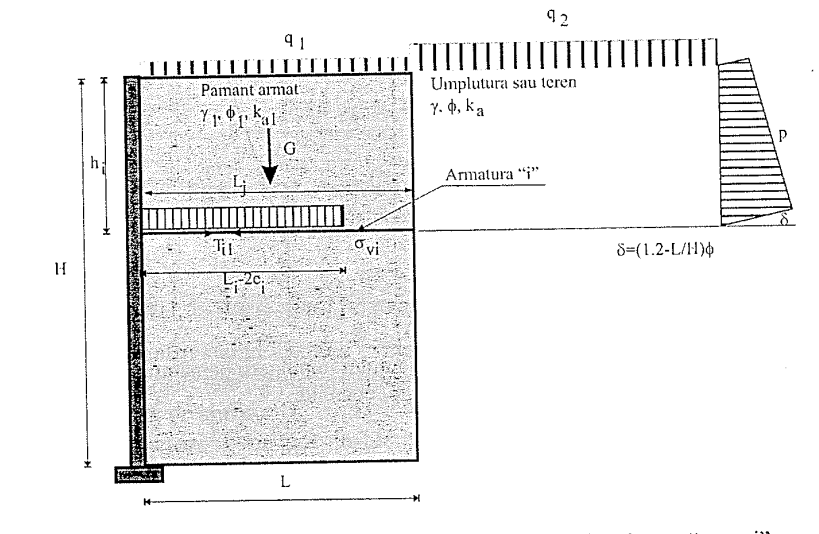
Figura 6.24. Schema de calcul pentru forța de întindere în armătura „i" datorată greutății proprii și suprasarcinii - metoda gravității coerente
b)Forța de întindere datorată sarcinilor concentrate verticale (date de fundații), Ti2 (Figura 6.25).
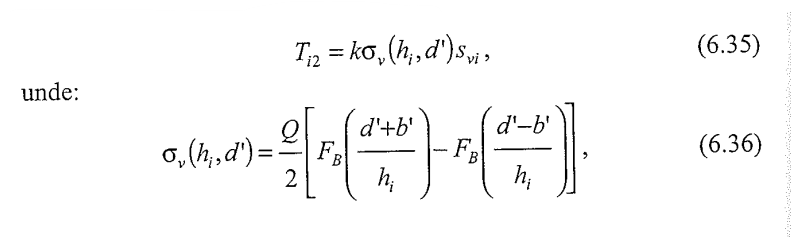
Unde:
FB este o funcție egală cu:
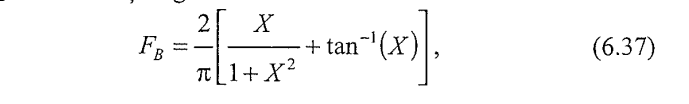
Cu tan-1(X) în radiani, unde X este egal cu:
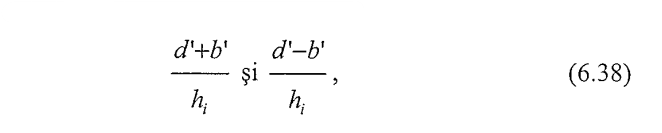
Q este presiunea pe talpa fundației,
svi este distanța pe verticală între armături la nivelul „i”.
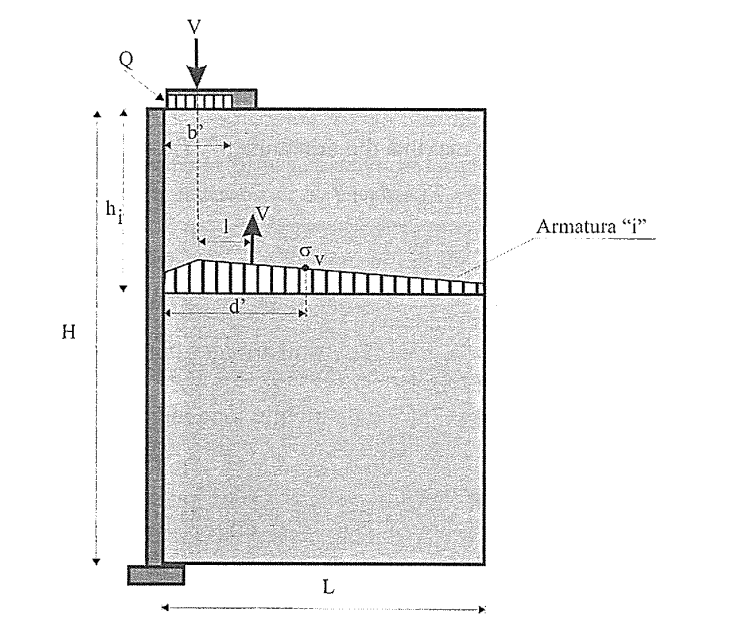
Figura 6.25. Schema de calcul pentru forța de întindere în armătura „i" datorată unei forțe concentrate verticale (fundație)- metoda gravității coerente
Pentru fiecare nivel hi se poate calcula σv pentru diferite valori ale distanței d', deoarece efortul vertical variază în lungul armăturii. Valoarea efortului σv considerată relevanta (de exemplu, cea maximă) va fi utilizată apoi pentru calculul forței de tracțiune în armătură.
c)Forța de întindere datorată sarcinilor concentrate orizontale (date de fundații de lățime b), Ti3 (Figura 6.26):
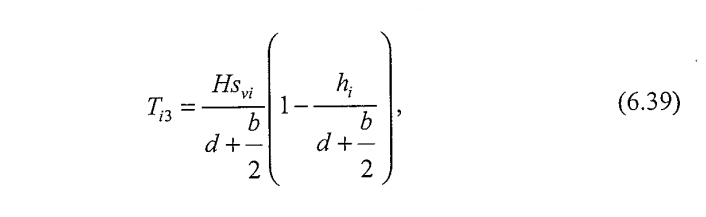
unde:
H este forța orizontală,
svi este distanța pe verticală între armături la nivelul „i".
Forța de întindere maximă din armătura „i", Ti este egală cu:
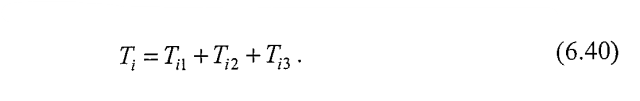
Valorile Ti2 și Ti3 nu iau în considerare o distribuție longitudinală a forțelor, paralelă cu fațada structurii. Pentru o analiză mai riguroasă se poate considera:
-pentru 0 < hi < 0.75L', o distribuție longitudinală cu o pantă de 1 : 4 (V: H),
-pentru hi > 0.75L', o distribuție longitudinală cu o pantă de 3 : 4 (V: H),
unde L' este lungimea fundației.
Linia de întindere maximă pentru o structură de sprijin armată cu materiale inextensibile poate fi considerată o spirală logaritmică (Figura 6.27).
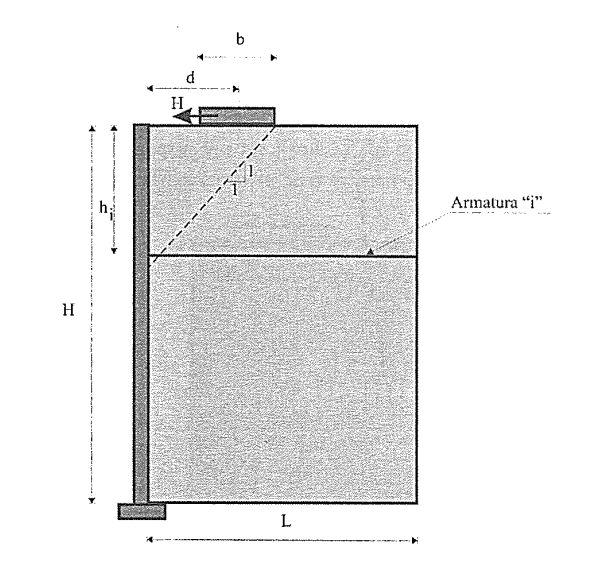
Figura 6.26. Schema de calcul pentru forța de întindere în armătura „i" datorată unei forțe concentrate orizontale (fundație) -metoda gravității coerente
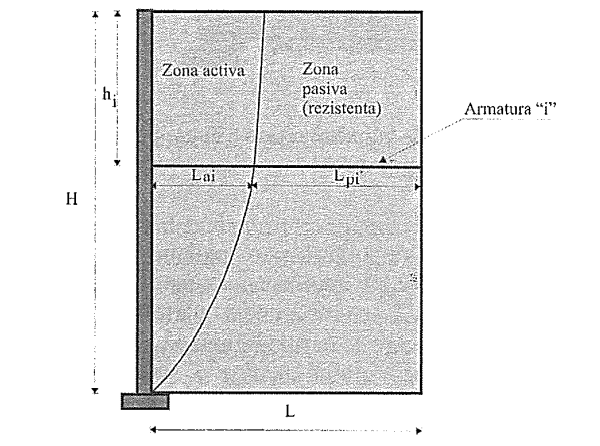
Figura 6.27. Linia de întindere maximă - metoda gravității coerente
Pentru calcul, în cazul în care nu există o fundație la partea superioară a structurii, această linie poate fi simplificată așa cum este arătat în Figura 6.28. Linia astfel obținută va fi numită „linia 2”.
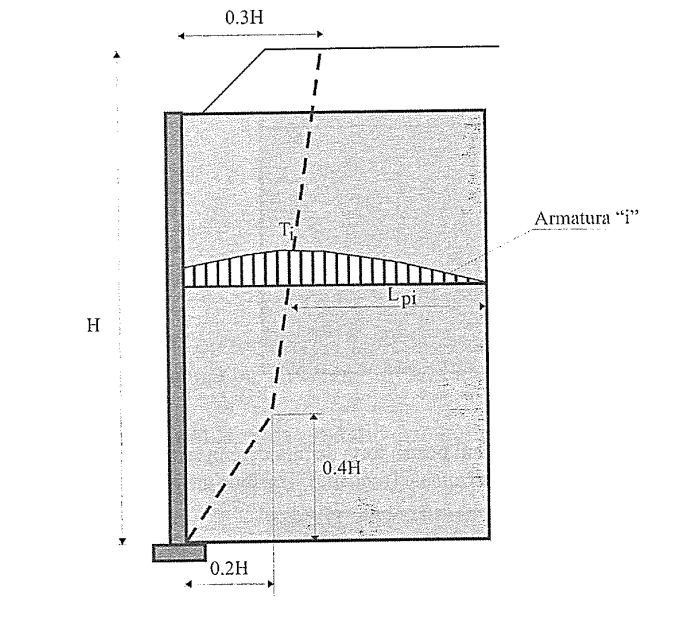
Figura 6.28. Linia de întindere maximă în cazul inexistenței unei fundații - metoda gravității coerente
Atunci când structura suportă și o fundație, existența acesteia influențează poziția liniei 2 de întindere maximă. Daca fundația este amplasată dincolo de linia 2, se presupune că partea superioară a liniei 2 se închide în punctul în care se termină fundația, fără însa a depăși o linie de tensiune maximă definită pentru o structură de înălțime echivalentă Hm, Hm este maximul dintre H și H1+ Qm / γ, unde Qm este presiunea medie pe o lățime egală cu 0,5H1 în spatele fațadei, calculată cu metoda Meyerhof (a se vedea și Figura 6.4).
În cazul existenței fundației la partea superioară a structurii, trebuie luat în considerare o a doua linie de întindere maximă, numită „linia 1" (Figura 6.29). Întinderea maximă într-o armătură se determină la intersecția fie cu linia 1, fie cu linia 2. Pentru calcul, se poate adopta simplificarea liniei 1 conform Figura 6.30.
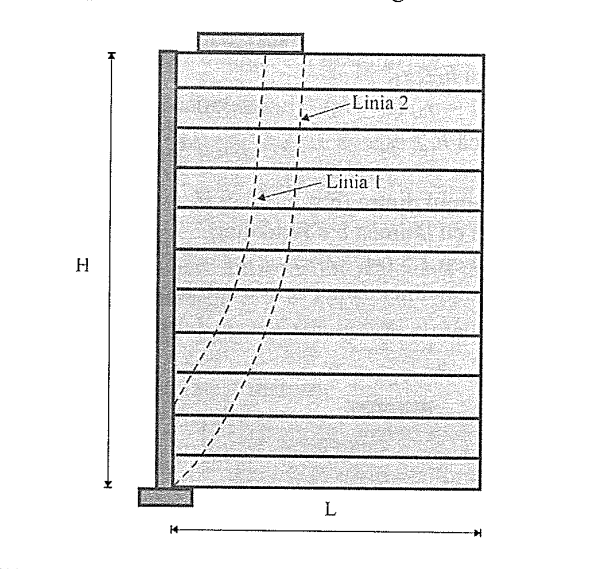
Figura 6.29. Linii de întindere maximă în cazul existenței unei fundații - metoda gravității coerente
Valoarea Ti calculată prin însumarea diverselor efecte reprezintă forța maximă de întindere în armături.
Forța de întindere variază însă de-a lungul armăturii, de aceea ea va fi calculată în 3 puncte:
-la nivelul fațadei:
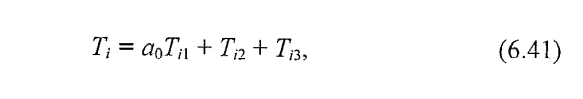
-de-a lungul liniei 1:
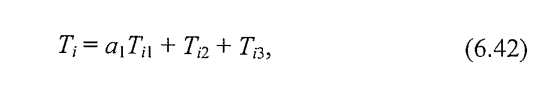
-de-a lungul liniei 2:

unde ao și a1 sunt variabile care iau următoarele valori în cazul unei fațade articulate:
a0 = 0.85, dacă hi ≤ z2, (6.44)
a0 = 1 - 0.15 (H1 - hi) / (H1 -z2), daca hi > z2, (6.45)
a1 = 1, dacă hi ≤ z1, (6.46)
a1 = a0 +(1 - a0) (z0 - hi) / (z0 -z1), dacă z1 < hi < z0, (6.47)
a1 = a0, dacă hi ≥ z0, (6.48)
unde:
z0 este minimul dintre (d + b / 2) și H1,
z1 este egal cu lățimea b a fundației,
z2 este egal cu 1.5 (H1 / 2- zactiv),
zactiv este adâncimea zonei active sub fundație.
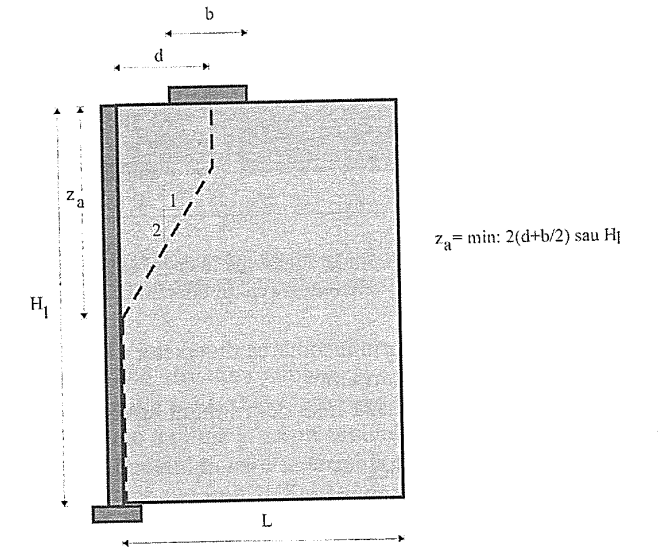
Figura 6.30. Definirea liniei 1 de întindere maximă - metoda gravității coerente
© GeoStru |