Las fuerzas agentes en el cuerpo resbaladizo incluyen el peso efectivo del terreno, W, las fuerzas sísmicas pseudo estáticas horizontales y verticales KxW y KYW, las fuerzas horizontales y verticales X y Y aplicadas externamente al perfil del talud, en fin, el resultado de los esfuerzos totales normales y de corte σ y τ agentes en la potencial superficie de deslizamiento.
El esfuerzo total normal puede incluir un exceso de presión de poros, u, que se debe especificar con la introducción de los parámetros de fuerza eficaz.
Prácticamente este método se puede considerar como una extensión del método del círculo de rozamiento en secciones homogéneas anteriormente descrito por Taylor.
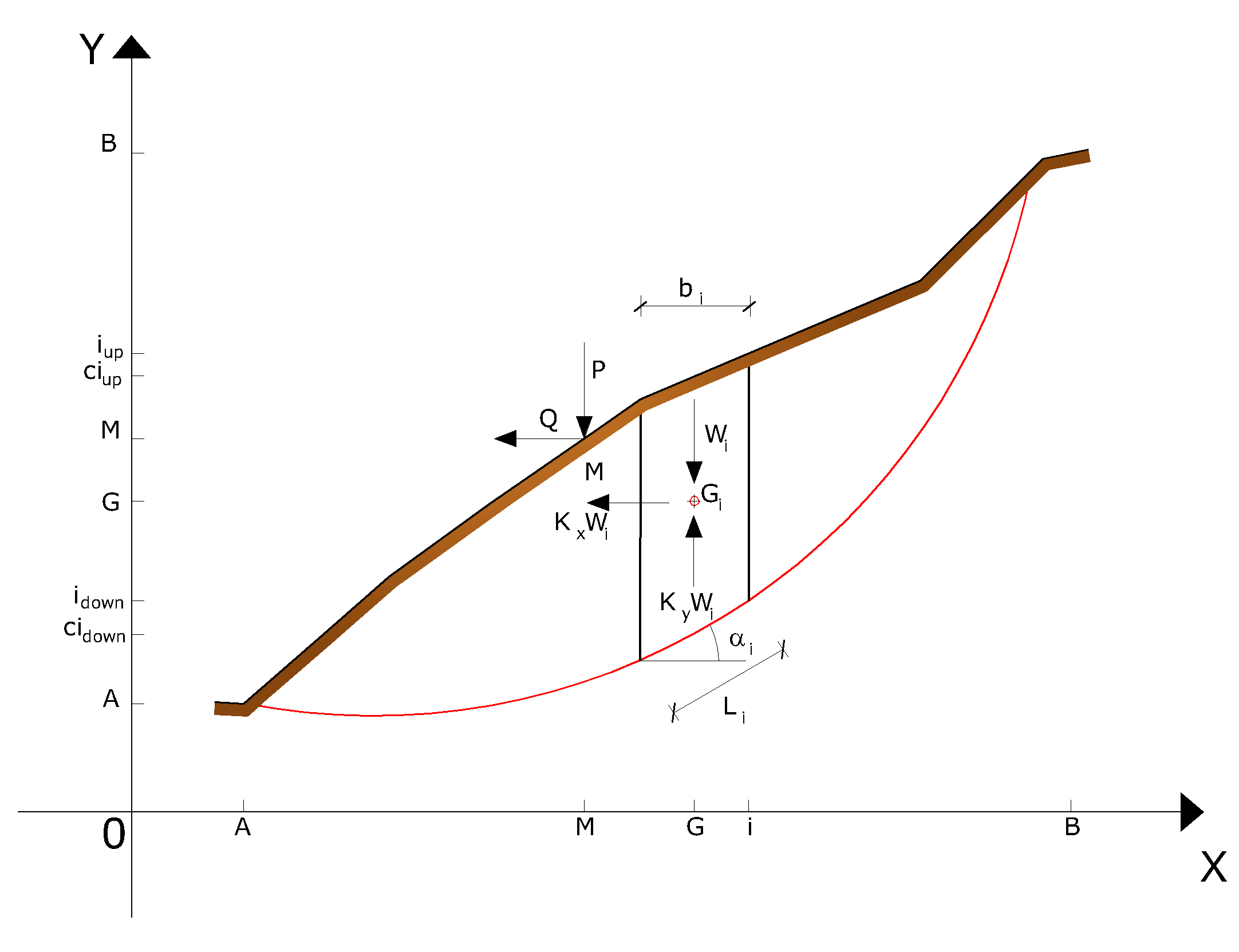
Representación, en el plano cartesiano, del conjunto y de las acciones agentes en la i-ésima rebanada
De acuerdo con la ley de la resistencia de Mohr-Coulomb en términos de tensión efectiva, la fuerza de corte agente en la base de la i-ésima rebanada está dada por:
![]()

donde:
F = factor de seguridad;
ci= cohesión eficaz (o total) en la base de la i-ésima rebanada;
φi = ángulo de rozamiento eficaz (= 0 con la cohesión total) en la base de la i-ésima rebanada;
Li = longitud de la base de la i-ésima rebanada;
μci =presión de los poros en el centro de la base de la i-ésima rebanada
El equilibrio se da igualando a cero la suma de las fuerzas horizontales, la suma de las fuerzas verticales y la suma de los momentos con respecto al origen.
Se adopta la siguiente asunción en la variación de la tensión normal agente en la potencial superficie de deslizamiento:
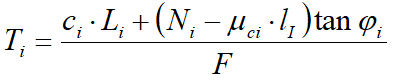
donde el primer término de la ecuación incluye la expresión:
Wi cos αi / Li= valor del esfuerzo normal total asociado al método ordinario de las rebanadas.
El segundo término de la ecuación incluye la función:
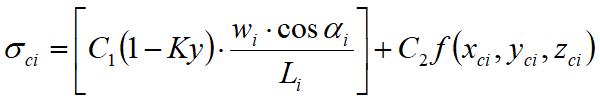
Donde x0 y xnson, respectivamente, las abscisas del primer y del último punto de la superficie de deslizamiento, mientras Xci representa la abscisa del punto medio de la base de la i-ésima rebanada.
Una parte sensible de reducción del peso asociada a una aceleración vertical del terreno Ky g se puede transmitir directamente a la base y esto se incluye en el factor (1 - Ky).
El esfuerzo normal total en la base de una rebanada se da con:
![]()
La solución de las ecuaciones de equilibrio se obtiene resolviendo un sistema lineal de tres ecuaciones obtenidas multiplicando las ecuaciones de equilibrio por el factor de seguridad F, sustituyendo la expresión de Ni y multiplicando cada término de la cohesión por un coeficiente arbitrario C3.
Se asume una relación de linealidad entre dicho coeficiente, determinable con la regla de Cramer, y el factor de seguridad F. El valor correcto de F se puede obtener con la fórmula de interpolación lineal:
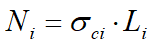
donde los números entre paréntesis (1) y (2) indican los valores iniciales y sucesivos de los parámetros F e C3.
Cualquier conjunto de valores del factor de seguridad alrededor de una estimación físicamente razonable se puede usar para iniciar una solución iterativa.
El número necesario de iteraciones depende ya sea de la estimación inicial que de la precisión deseada de la solución; normalmente el proceso converge rápidamente.
© GeoStru Software