El método de Sarma es un simple pero esmerado método para el análisis de estabilidad de taludes que permite determinar la aceleración sísmica horizontal necesaria para que la masa de terreno, delimitada por la superficie de deslizamiento y por el perfil topográfico, alcance el estado de equilibrio límite (aceleración crítica Kc) y, al mismo tiempo, permite obtener el factor de seguridad obtenido como con los otros métodos comunes de la geotecnia.
Se trata de un método basado en el principio del equilibrio límite y de las franjas. Por lo tanto se considera el equilibrio de una masa potencial de terreno en deslizamiento subdividida en n franjas verticales de espesor suficientemente pequeño como para asumir que el esfuerzo normal Ni obra en el punto medio de la base de la franja.
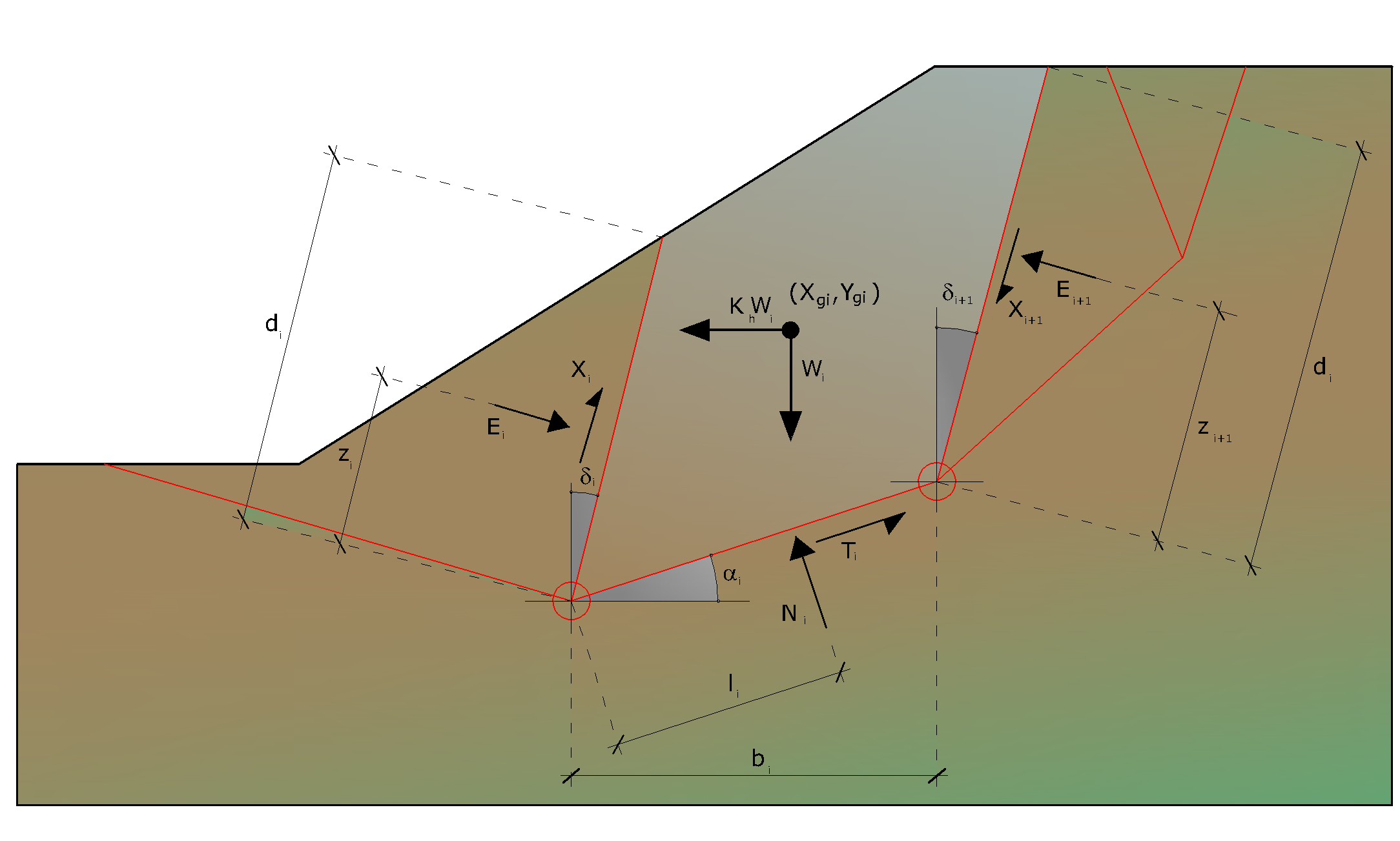
Acciones en la i-ésima rebanada, método de Sarma
Las ecuaciones que se deben tener en consideración son:
•La ecuación de equilibrio en la traslación horizontal de cada rebanada;
•La ecuación de equilibrio en la traslación vertical de cada rebanada;
•La ecuación de equilibrio de momentos.
Condiciones de equilibrio en la traslación horizontal y vertical:
Ni cos αi + Ti sin αi = Wi - ΔXi
Ti cos αi - Ni sin αi = KWi +ΔEi
Además se asume que en ausencia de fuerzas externas en la superficie libre se tiene:
ΣΔEi = 0
ΣΔXì = 0
donde Eì y Xi representan, respectivamente, las fuerzas horizontales y verticales en la i-ésima cara de la rebanada genérica i.
La ecuación de equilibrio de momentos se escribe seleccionando como punto de referencia el baricentro del cúmulo; de manera que, después de haber efectuado una serie de posiciones y transformaciones trigonométricas y algebraicas, en el método de Sarma la solución del problema se obtiene resolviendo dos ecuaciones:
![]()
![]()
Pero el enfoque de solución, en este caso, está completamente invertido: el problema en efecto requiere encontrar un valor de K (aceleración sísmica) correspondiente a un determinado factor de seguridad; y en particular, encontrar el valor de la aceleración K correspondiente al factor de seguridad F = 1, o sea la aceleración crítica.
Se obtiene por lo tanto:
K = Kc aceleración crítica si F = 1
F = Fs factor de seguridad en condiciones estáticas si K = 0
La segunda parte del problema del Método de Sarma es encontrar una distribución de fuerzas internas Xi y Ei tal que permita verificar el equilibrio de la rebanada y el equilibrio global del macizo, sin violar el criterio de rotura.
Se ha encontrado que una solución aceptable al problema se puede obtener asumiendo la siguiente distribución de las fuerzas Xi:
![]()
donde Qi es una función conocida, donde se toman en cuenta los parámetros geotécnicos promedio en la i-ésima cara de la rebanada i, y l representa una incógnita.
La solución completa del problema se obtiene por lo tanto, después de algunas iteraciones, con los valores de Kc, l y F, que permiten obtener también la distribución de las fuerzas entre las franjas.
© GeoStru Software