Janbu estese il metodo di Bishop a superfici si scorrimento di forma qualsiasi.
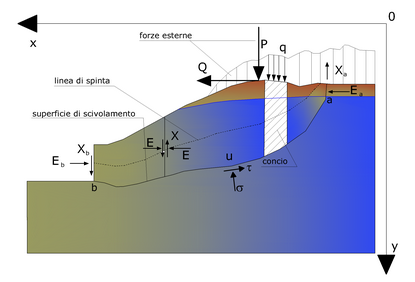
Quando vengono trattate superfici di scorrimento di forma qualsiasi il braccio delle forze cambia (nel caso delle superfici circolari resta costante e pari al raggio) a tal motivo risulta più conveniente valutare l’equazione del momento rispetto allo spigolo di ogni blocco.
Con il metodo di Janbu si tiene conto delle forze di interazione tra i conci, ma si considera che esse agiscono lungo una linea di spinta prefissata. La soluzione si ottiene per successive iterazioni.
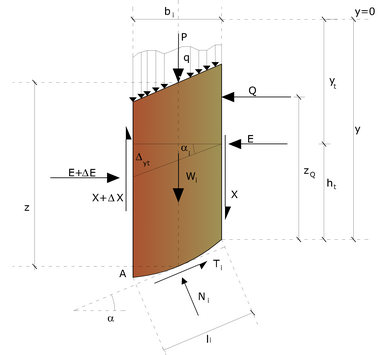
Facendo riferimento allo schema illustrato in figura in alto, le assunzioni che stanno alla base del procedimento proposto da Janbu (1973) sono le seguenti:
- si suppone nota la linea di azione delle forze E che si scambiano i vari conci;
- la risultante Ni agisce nel punto in cui la retta di azione di (Wi + q · bi + P) intercetta la base del concio.
Le incognite del problema nel caso più generale sono: E, X, Ni, Ti.
L'equilibrio alla traslazione verticale di un concio può esprimersi nella forma:
Ni · cosα + Ti · sinα = Wi + P + q · bi + ΔT
L'equilibrio alla traslazione orizzontale di un concio può esprimersi nella forma:
ΔE + Ti · cosα = Q + Ni · sinα
La combinazione di tali equazioni con l'equazione dell'equilibrio globale permettono di calcolare, per ogni superficie ipotizzata, il valore del coefficiente di sicurezza F, procedendo per successive iterazioni:
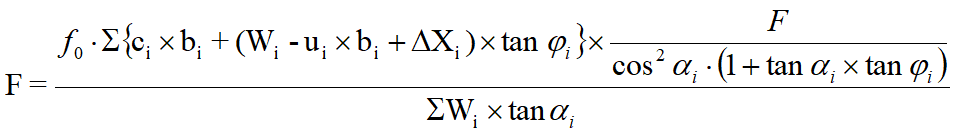
|
|
Azioni sul concio i-esimo secondo le ipotesi di Janbu e rappresentazione d'insieme dell'ammasso
Assumendo ΔXi= 0 si ottiene il metodo ordinario.
Il confronto tra i valori di F relativi a successive iterazioni serve infine a stabilire la precisione raggiunta. A tal proposito Janbu propose un metodo per la correzione del fattore di sicurezza ottenuto con il metodo ordinario secondo la seguente equazione:
Fcorretto = f0 F
|
|
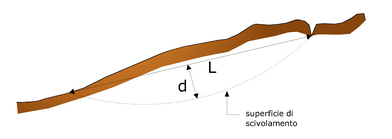
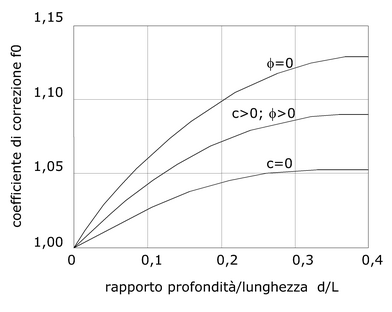
Calcolo del fattore correttivo f0
dove fo, fattore di correzione empirico, dipende dalla forma della superficie di scivolamento e dai parametri geotecnici. Tale correzione è molto attendibile per pendii poco inclinati.
© GeoStru