Le forze agenti sul corpo che scivola includono il peso effettivo del terreno, W, le forze sismiche pseudostatiche orizzontali e verticali KXW e KYW, le forze orizzontali e verticali X e Y applicate esternamente al profilo del pendio, infine, la risultante degli sforzi totali normali e di taglio σ e τ agenti sulla superficie potenziale di scivolamento. Lo sforzo totale normale può includere un eccesso di pressione dei pori u che deve essere specificata con l’introduzione dei parametri di forza efficace. In pratica questo metodo può essere considerato come un’estensione del metodo del cerchio di attrito per sezioni omogenee precedentemente descritto da Taylor.
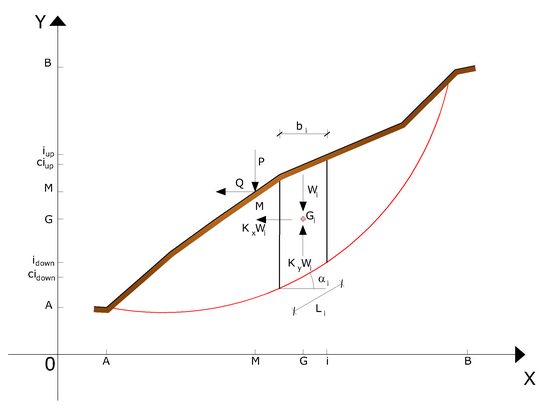
Rappresentazione su piano cartesiano dell'ammasso e delle azioni agenti sul concio i-esimo
In accordo con la legge della resistenza di Mohr-Coulomb in termini di tensione efficace, la forza di taglio agente sulla base dell’i-esimo concio è data da:
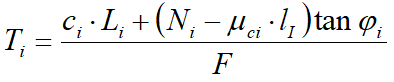
in cui
F = fattore di sicurezza;
ci = coesione efficace (o totale) alla base dell’i-esimo concio;
φi = angolo di attrito efficace (= 0 con la coesione totale) alla base dell’i-esimo concio;
Li = lunghezza della base dell’i-esimo concio;
μci = pressione dei pori al centro della base dell’i-esimo concio.
L’equilibrio risulta uguagliando a zero la somma delle forze orizzontali, la somma delle forze verticali e la somma dei momenti rispetto all’origine.
Viene adottata la seguente assunzione sulla variazione della tensione normale agente sulla potenziale superficie di scorrimento:
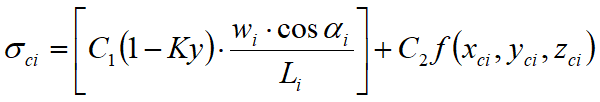
in cui il primo termine dell’equazione include l’espressione:
Wi cos αi / Li = valore dello sforzo normale totale associato con il metodo ordinario dei conci.
Il secondo termine dell’equazione include la funzione:
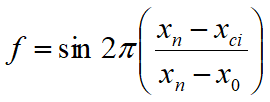
Dove x0 ed xn sono rispettivamente le ascisse del primo e dell’ultimo punto della superficie di scorrimento, mentre xci rappresenta l’ascissa del punto medio della base del concio i-esimo.
Una parte sensibile di riduzione del peso associata con una accelerazione verticale del terreno Ky g può essere trasmessa direttamente alla base e ciò è incluso nel fattore (1 - Ky).
Lo sforzo normale totale alla base di un concio è dato da:
![]()
La soluzione delle equazioni di equilibrio si ricava risolvendo un sistema lineare di tre equazioni ottenute moltiplicando le equazioni di equilibrio per il fattore di sicurezza F, sostituendo l’espressione di Ni e moltiplicando ciascun termine della coesione per un coefficiente arbitrario C3.
Si assume una relazione di linearità tra detto coefficiente, determinabile tramite la regola di Cramer, ed il fattore di sicurezza F. Il corretto valore di F può essere ottenuto dalla formula di interpolazione lineare:
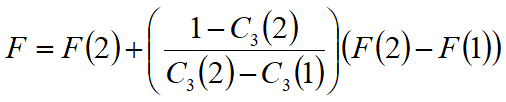
dove i numeri in parentesi (1) e (2) indicano i valori iniziale e successivo dei parametri F e C3. Qualsiasi coppia di valori del fattore di sicurezza nell’intorno di una stima fisicamente ragionevole può essere usata per iniziare una soluzione iterativa.
Il numero necessario di iterazioni dipende sia dalla stima iniziale sia dalla desiderata precisione della soluzione; normalmente, il processo converge rapidamente.
© GeoStru