Il metodo di Sarma è un semplice, ma accurato metodo per l’analisi di stabilità dei pendii, che permette di determinare l'accelerazione sismica orizzontale richiesta affinché l’ammasso di terreno, delimitato dalla superficie di scivolamento e dal profilo topografico, raggiunga lo stato di equilibrio limite (accelerazione critica Kc) e, nello stesso tempo, consente di ricavare l’usuale fattore di sicurezza ottenuto come per gli altri metodi più comuni della geotecnica.
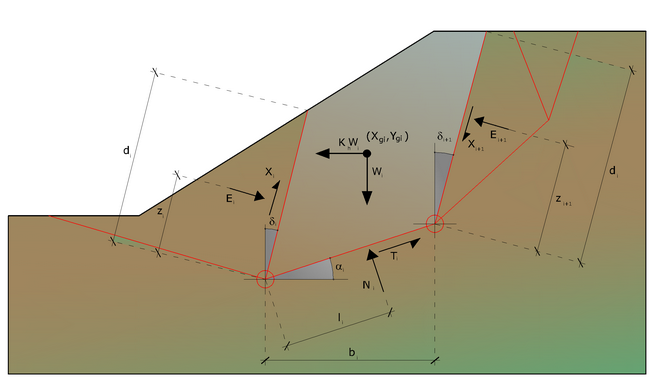
Si tratta di un metodo basato sul principio dell’equilibrio limite e delle strisce, pertanto viene considerato l’equilibrio di una potenziale massa di terreno in scivolamento suddivisa in n strisce verticali di spessore sufficientemente piccolo da ritenere ammissibile l’assunzione che lo sforzo normale Ni agisce nel punto medio della base della striscia.
Le equazioni da prendere in considerazione sono:
•L'equazione di equilibrio alla traslazione orizzontale del singolo concio;
•L'equazione di equilibrio alla traslazione verticale del singolo concio;
•L'equazione di equilibrio dei momenti.
Condizioni di equilibrio alla traslazione orizzontale e verticale:
Ni cos αi + Ti sin αi = Wi - ΔXi
Ti cos αi - Ni sin αi = KWi +ΔEi
Viene, inoltre, assunto che in assenza di forze esterne sulla superficie libera dell’ammasso si ha:
ΣΔEi = 0
ΣΔXì = 0
dove Eì e Xi rappresentano, rispettivamente, le forze orizzontale e verticale sulla faccia i-esima del concio generico i.
L’equazione di equilibrio dei momenti viene scritta scegliendo come punto di riferimento il baricentro dell’intero ammasso; sicché, dopo aver eseguito una serie di posizioni e trasformazioni trigonometriche ed algebriche, nel metodo di Sarma la soluzione del problema passa attraverso la risoluzione di due equazioni:
![]()
![]()
Ma l’approccio risolutivo, in questo caso, è completamente capovolto: il problema infatti impone di trovare un valore di K (accelerazione sismica) corrispondente ad un determinato fattore di sicurezza; ed in particolare, trovare il valore dell’accelerazione K corrispondente al fattore di sicurezza F = 1 , ossia l’accelerazione critica.
Si ha pertanto:
K = Kc accelerazione critica se F = 1
F = Fs fattore di sicurezza in condizioni statiche se K = 0
La seconda parte del problema del Metodo di Sarma è quella di trovare una distribuzione di forze interne Xi ed Ei tale da verificare l’equilibrio del concio e quello globale dell’intero ammasso, senza violazione del criterio di rottura.
E’ stato trovato che una soluzione accettabile del problema si può ottenere assumendo la seguente distribuzione per le forze Xi:
![]()
dove Qi è una funzione nota, in cui vengono presi in considerazione i parametri geotecnici medi sulla i-esima faccia del concio i, e λ rappresenta un’incognita.
La soluzione completa del problema si ottiene pertanto, dopo alcune iterazioni, con i valori di Kc, l e F, che permettono di ottenere anche la distribuzione delle forze di interstriscia.
© GeoStru