Il metodo è basato sull’assunzione:
Le forze d’interfaccia lungo le superfici di divisione dei singoli conci sono orientate parallelamente fra loro ed inclinate rispetto all’orizzontale di un angolo q tutti i momenti sono nulli Mi =0 i=1…..n
Sostanzialmente il metodo soddisfa tutte le equazioni della statica ed equivale al metodo di Morgenstern e Price quando la funzione f(x) = 1.
Imponendo l’equilibrio dei momenti rispetto al centro dell’arco descritto dalla superficie di scivolamento si ha:
|
(1) |
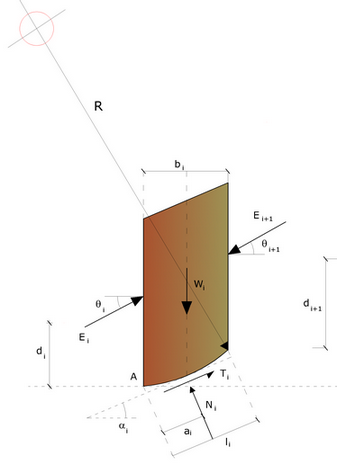
Azioni sul concio i-esimo secondo le ipotesi di Spencer
dove:
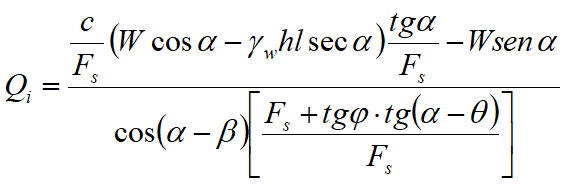
forza d’interazione fra i conci;
R = raggio dell’arco di cerchio;
θ = angolo d’inclinazione della forza Qi rispetto all’orizzontale.
Imponendo l’equilibrio delle forze orizzontali e verticali si ha rispettivamente:
|
(2) |
Con l’assunzione delle forze Qi parallele fra loro, si può anche scrivere:
![]()
Il metodo propone di calcolare due coefficienti di sicurezza: il primo (Fsm) ottenibile dalla (1), legato all’equilibrio dei momenti; il secondo (Fsf) dalla (2) legato all’equilibrio delle forze. In pratica si procede risolvendo la (1) e la (2) per un dato intervallo di valori dell’angolo θ, considerando come valore unico del coefficiente di sicurezza quello per cui si abbia
Fsm = Fsf
© GeoStru