<< Click to Display Table of Contents >> Navigation:  Slope > Sovrappressioni interstiziali

 

 

 

Resistenza a taglio in condizioni di carico sismico

In assenza di determinazioni sperimentali appropriate, ottenute da prove di cicliche di laboratorio, la riduzione di resistenza al taglio in condizioni di carico sismico può essere stimata avvalendosi di relazioni empiriche di letteratura, come indicato nei paragrafi seguenti, con riferimento al caso di analisi condotte in termini di tensioni efficaci o in termini di tensioni totali.

 

 

Analisi in condizioni di tensioni efficaci

L’incremento di pressione interstiziale deve essere valutato nel caso di terreni saturi se la deformazione di taglio indotta dall’azione sismica è superiore al valore della deformazione di soglia volumetrica, γv. Nei terreni parzialmente saturi, la pressione interstiziale aumenta durante l’applicazione della sollecitazione sismica, ma si mantiene generalmente inferiore alla pressione atmosferica; in tal caso, può essere assunto un valore nullo delle pressioni interstiziali per tutto il periodo di applicazione del carico (σ’=s) e le analisi possono essere eseguite utilizzando le caratteristiche di resistenza determinate in prove drenate eseguite su provini preventivamente saturati dello stesso materiale. Per la valutazione di Du è opportuno distinguere il comportamento delle terre in relazione alla loro diversa natura, coesiva o incoerente.

 

Terreni coesivi

Nei terreni coesivi, l’incremento di pressione interstiziale Δu, ad una certa profondità, può essere stimato mediante la seguente relazione empirica (Matsui et al., 1980):

Dove σ’0 è il valore iniziale della pressione media efficace alla profondità considerata, γc,max è la deformazione di taglio massima raggiunta durante il sisma e β=0.45 è un coefficiente sperimentale. La deformazione di soglia volumetrica γv, determinabile con prove cicliche di laboratorio, può essere valutata in prima approssimazione mediante la relazione:

Nella quale OCR è il grado di sovraconsolidazione, A e B sono coefficienti sperimentali che, in assenza di una determinazione diretta, possono essere ricavati in funzione dell’ indice di plasticità vedi Tab. 4.17.1:

Tabella 4.17.1: Valori suggeriti per i coefficienti A e B

 

 

Il valore di γc,max relativo alla profondità considerata può essere determinato mediante un analisi della risposta sismica locale. In alternativa, si determina preliminarmente il valore di τmax mediante la relazione empirica:

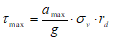
Dove amax, espressa in g, è l’accelerazione di picco al piano campagna sulla verticale relativa al punto considerato; g è l’accelerazione di gravità; σv è la tensione verticale totale; rd è un coefficiente riduttivo che tiene conto dell’azione sismica alla profondità di interesse che porta in conto la deformabilità del sottosuolo. Il coefficiente rd può essere valutato, in prima approssimazione, con la seguente espressione:

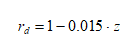
Dove z è la profondità nel punto considerato. La massima deformazione di taglio indotta dal sisma si ricava quindi dalla relazione:

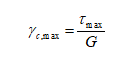
Dove il modulo di taglio G può essere determinato, per via iterativa, dalla curva (G-γ) ottenuta da prove di laboratorio.

 

 

Terreni granulari

Nei terreni granulari, l’incremento di pressione interstiziale generato dalla sollecitazione sismica può essere stimato mediante la seguente relazione empirica (Seed & Booker, 1997):

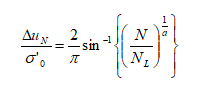
Dove ΔuN è l’incremento di pressione interstiziale dopo N cicli di carico, σ’0 il valore iniziale della pressione media efficace alla profondità considerata, N è il numero di cicli di carico di ampiezza costante equivalente al sisma ed NL è il numero di cicli di carico necessari per produrre la liquefazione nel terreno. La costante sperimentale a può essere valutata mediante la relazione proposta da Fardis & Veneziano (1981) in funzione della densità relativa Dr (in frazione):

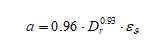
Il termine εq ha distribuzione log-normale con valore medio unitario e varianza pari a 0.1. Per determinare il numero di cicli N che compare in una delle relazioni precedenti è necessario approssimare la storia deformativi di taglio irregolare indotta dal terremoto con una sollecitazione ciclica equivalente di ampiezza costante (τeq) e numero di cicli equivalente (Neq) seguendo una delle numerose procedure presenti in letteratura. Utilizzando ad esempio la procedura proposta da Biondi et al. (2004) si ottiene:

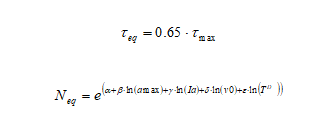
Nella prima delle equazioni precedenti τmax rappresenta la sollecitazione di taglio massima indotta dal terremoto alla profondità considerata, il cui valore può essere stimato mediante un analisi della risposta sismica locale o, in prima approssimazione mediante la relazione utilizzata nel paragrafo relativo ai terreni coesivi. Nella seconda delle equazioni precedenti i vari termini hanno il seguente significato:

 

-Ia:  è l’intensità di Arias (m/s);

-v0: è l’intensità degli incroci con l’asse dei tempi dell’accelerogramma (s-1);

-TD: è la durata dell’ accelerogramma definita da Trifunac e Brady (s);

 

L’intensità di Arias è definita mediante la seguente formula:

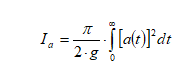
Gli altri simboli che compaiono, ossia α - β - γ - δ - ε, sono delle costanti per le quali sono consigliati i seguenti valori:

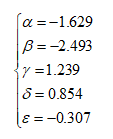
Per la determinazione del valore di NL si può fare riferimento a metodi che poggiano su interpolazioni di tipo grafico, o eventualmente si possono utilizzare i risultati di prove triassali cicliche o di taglio semplice ciclico.

 

 

©  GeoStru