La forza di trazione agente sul singolo chiodo, F_i, può essere valutata mediante la seguente espressione, valida in presenza di falda, in condizioni pseudo-statiche e terreno omogeneo:
|
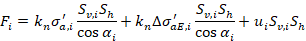 |
(4) |
In cui i vari termini assumono le seguenti espressioni:
kn: coefficiente riduttivo
σa,i': tensione efficacie attiva alla profondità media della zona di influenza dell’i-esimo chiodo
Sv,i: interasse tra i chiodi nella direzione verticale; definisce anche lo spessore della zona di influenza dell’i-esimo chiodo
Sh: interasse tra i chiodi nella direzione orizzontale
αi: inclinazione, rispetto alla direzione orizzontale, dell’i-esimo chiodo
∆σaE,i': incremento della tensione efficacie attiva alla profondità media della zona di influenza dell’i-esimo chiodo per effetto del sisma
ui: pressione neutra alla profondità media della zona di influenza dell’i-esimo chiodo
La tensione efficacie attiva è calcolata in funzione del coefficiente di spinta attiva, Ka, della tensione efficacie verticale agente alla profondità del punto considerato, σv,i', dell’eventuale carico q applicato sul terrapieno e della coesione efficacie c':
|
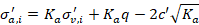 |
(5) |
Nel seguito, il coefficiente di spinta attiva viene calcolato mediante le seguenti teorie:
teoria di Rankine:
|
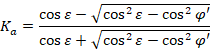 |
(6) |
teoria di Coulomb:
|
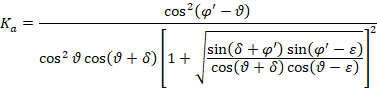 |
(7) |
In cui δ rappresenta l’angolo di attrito muro-terreno, mentre θ, definito in Fig. 2, deve essere utilizzato nell’Eq. 7 con segno negativo. Tutti gli altri parametri sono stati introdotti in precedenza. Per quanto riguarda l’incremento di tensione per effetto del sisma, viene calcolato nel modo seguente:
|
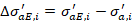 |
(8) |
In cui σaE,i' rappresenta la tensione efficacie alla profondità media della zona di influenza dell’i-esimo chiodo per effetto del sisma:
|
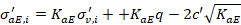 |
(9) |
In cui KaE è il coefficiente di spinta attiva nella condizione sismica, calcolato nel seguito mediante la teoria di Mononobe-Okabe:
|
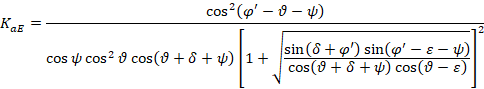 |
(10) |
In cui
|
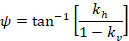 |
(11) |
È opportuno notare che nell’Eq. 4, la somma tra il primo ed il secondo termine potrebbe essere sostituita utilizzando l’Eq. 8. Tuttavia, si è preferito mantenere separato il contributo statico dall’incremento dovuto al sisma, poiché nel caso in cui si voglia applicare un approccio di normativa, è possibile moltiplicare i due termini per coefficienti differenti.
In caso di analisi eseguita in condizioni statiche, il secondo termine dell’Eq. 4 si annulla, mentre nel caso di terreno asciutto si annulla il terzo termine e nel primo la tensione efficacie coincide con quella totale.
Nel caso più generale, in cui il terreno è stratificato, a seconda della posizione dello spessore di influenza di ciascun chiodo rispetto agli strati di terreno, sono possibili i diversi quattro casi indicati in Fig. 5.
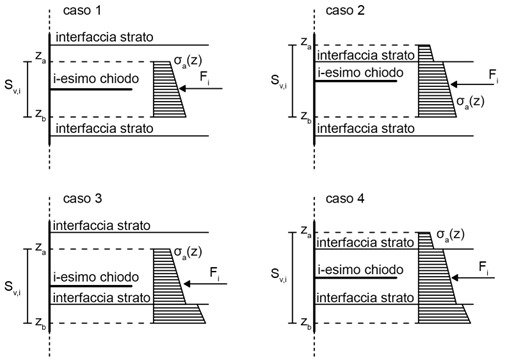
Fig. 5 – Possibili distribuzioni della tensione orizzontale totale, σa (z), con la profondità a seconda della posizione dello spessore di influenza di ciascun chiodo rispetto agli strati di terreno.
Con riferimento ad ognuno di tali casi, la Fig. 5 mostra l’andamento con la profondità della tensione orizzontale totale, σa (z), la quale è caratterizzata da un salto e da un cambio di pendenza in corrispondenza delle interfacce tra gli strati. Per situazioni del genere, è comodo calcolare la forza di trazione agente sul singolo rinforzo come la risultante della distribuzione delle tensioni orizzontali:
|
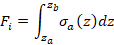 |
(12) |
In cui za e zb sono le profondità che definiscono l’inizio e la fine della zona di influenza dell’i-esimo chiodo. In condizioni pseudostatiche, nell’Eq. 12 è necessario aggiungere il termine dovuto all’incremento di tensione per effetto del sisma, utilizzando la stessa logica vista per il caso di terreno omogeneo.
©GeoStru