Se establece una relación, entre los componentes de las fuerzas de interconexión, de tipo X= λ f(x) E, donde λ es un factor de escala y f(x), que está en función de la posición de E y de X, establece una relación entre las variaciones de la fuerza X y de la fuerza E en la masa deslizante. La función f(x) se elige arbitrariamente (constante, sinusoide, semisinusoide, trapecio, fraccionada) e influye poco sobre el resultado, pero se debe verificar que los valores obtenidos de las incógnitas sean físicamente aceptables.
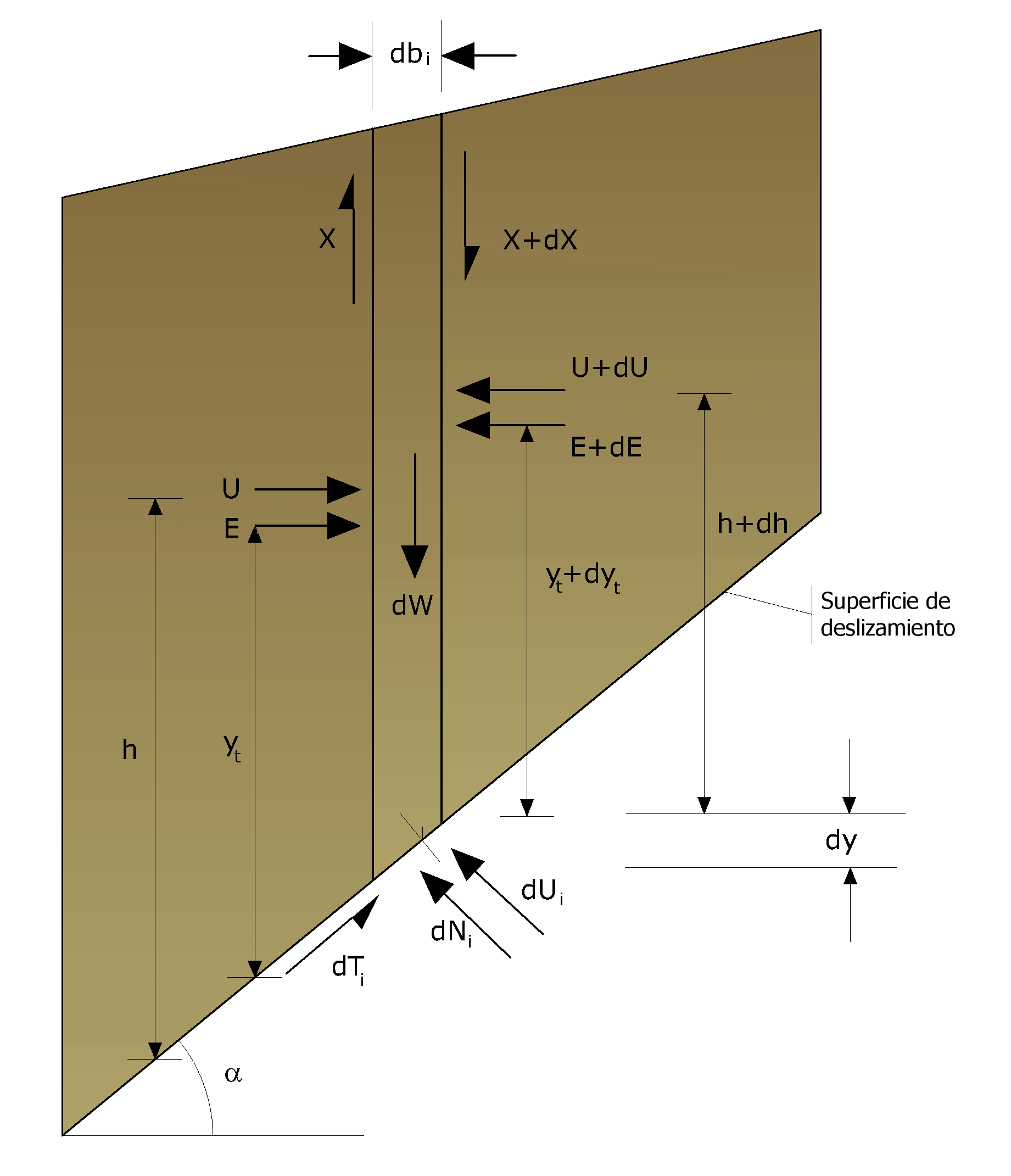
La particularidad del método es que la masa se subdivide en franjas infinitesimales, a las cuales se aplican las ecuaciones de equilibrio en la traslación horizontal y vertical y de rotura en la base de las franjas. Se llega a una primer ecuación diferencial que une las fuerzas de conexión incógnitas E, X, el coeficiente de seguridad Fs, el peso de la franja infinitésima dW y el resultado de las presiones neutras en la base dU.
|
|
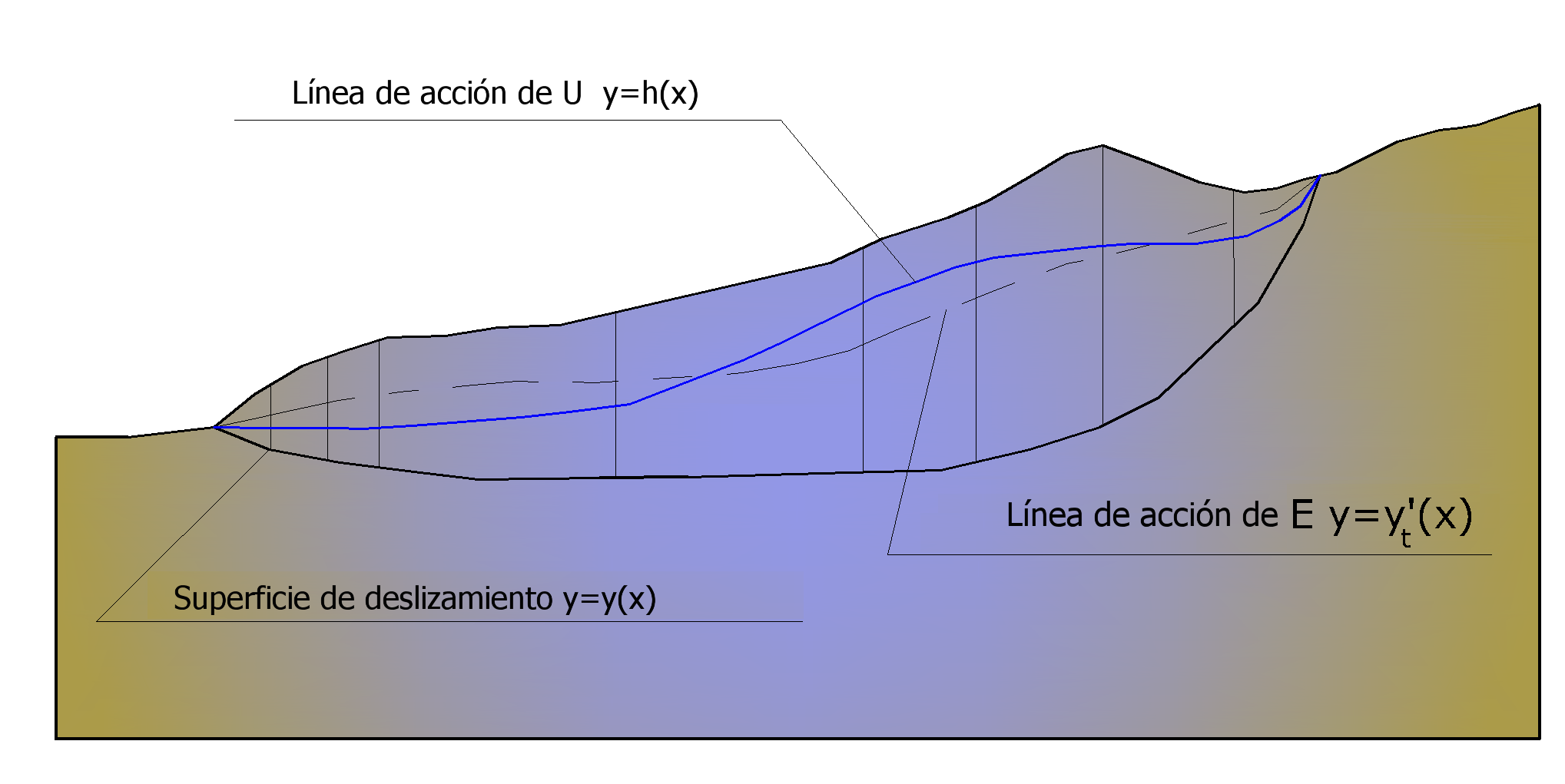
Acciones en la i-ésima rebanada según las hipótesis de Morgenstern y Price y representación del conjunto
Se obtiene la llamada “ecuación de las fuerzas”:

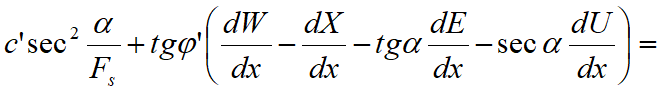
Una segunda ecuación, llamada “ecuación de los momentos”, se escribe imponiendo la condición de equilibrio a la rotación respecto a la base:
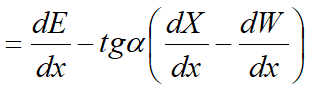
Estas dos ecuaciones se extienden por integración a toda la masa deslizante.
El método de cálculo satisface todas las ecuaciones de equilibrio y se aplica a superficies de cualquier forma, pero implica necesariamente el uso de un ordenador.
© GeoStru Software