Forțele ce acționează pe corpurile în alunecare includ greutatea efectivă a terenului, W, forțele seismice pseudostatice orizontale și verticale KxW și KyW, forțele orizontale și verticale X și Y aplicate extern asupra profilului taluzului și rezultanta eforturilor totale normale de forfecare σ și τ ce acționează pe suprafața potențial de alunecare.
Efortul total normal poate include un exces de presiune în pori u care trebuie să fie specificată la introducerea parametrilor de forță efectivă.
Practic această metodă poate fi considerată o extensie a metodei cercului de frecare pentru secțiuni omogene descrise anterior de către Taylor.
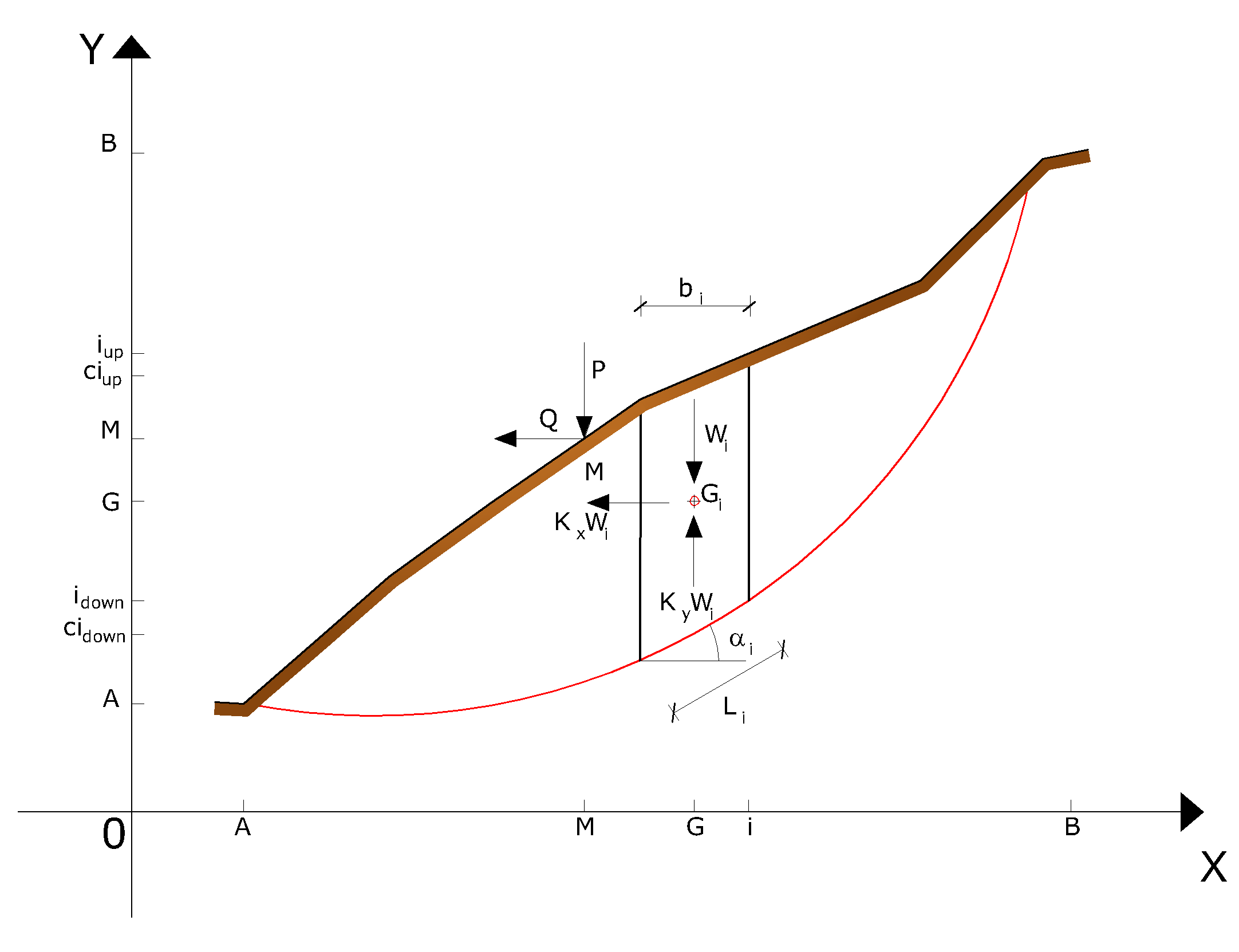
Reprezentarea pe plan cartezian a fâșiei și a acțiunilor ce acționează pe fâșia i
Conform legii de rezistență Mohr-Coulomb în termeni de tensiune efectivă, forța de forfecare ce acționează aspra bazei fâșiei este dată de:
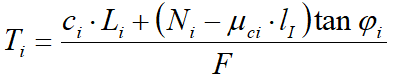
în care
F factorul de siguranță;
ci coeziunea efectivă (sau totală) la baza fâșiei i;
φi unghiul de frecare efectiv (= 0 cu coeziune totală) la baza fâșiei;
Li lungimea bazei fâșiei i;
μci presiunea în porii în centrul bazei fâșiei i.
Echilibrul se obține egalând cu zero suma forțelor orizontale, suma forțelor verticale și suma momentelor față de origine.
Este adoptată următoarea presupunere aspra variației tensiunii normale ce acționează pe suprafața potențială de alunecare:
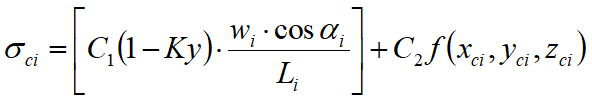
în care primul termen al ecuației include expresia:
•Wi cos αi / Li = valoarea efortului normal total cu metoda obișnuită a fâșiei.
Cel de-al doilea termen al ecuației include funcția:
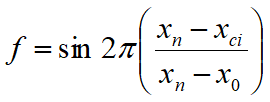
Unde x0 și xn sunt abscisele primului și ultimului punct ale suprafeței de alunecare, în timp ce xci reprezintă abscisa punctului mediu al bazei fâșiei i.
O parte sensibilă la reducerea greutății asociată cu o accelerație verticală a terenului Ky g poate fi transmisă direct bazei și este inclusă în factorul (1 - Ky).
Efortul normal total la baza unei fâșii este dat de:
![]()
Soluția ecuațiilor de echilibru se află rezolvând un sistem liniar de trei ecuații obținute multiplicând ecuațiile de echilibru cu factorul de siguranță F, înlocuind expresia lui Ni și înmulțind fiecare termen al coeziunii cu un coeficient arbitrar C3.
Se presupune o relație liniară între coeficientul de mai sus, determinabil prin regula lui Cramer, și factorul de siguranță F. Valoarea corectă a lui F poate fi obținută din formula de interpolare liniară:
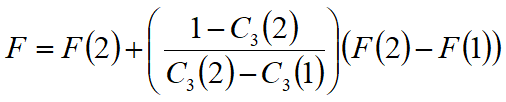
unde numerele dintre paranteze (1) și (2) indică valorile inițiale și următoare ale parametrilor F și C3.
Orice cuplu de valori ale factorului de siguranță în vecinătatea unei estimări rezonabile fizic poate fi folosit pentru a iniția o soluție iterativă.
Numărul necesar de iterații depinde atât de estimarea inițială cât și de precizia dorită a soluției.
© GeoStru