Metoda Sarma este o metodă simplă dar precisă pentru analiza stabilității taluzurilor, ce permite determinarea accelerației seismice orizontale cerute până în momentul în care terenul, delimitat de suprafață de alunecare și de profilul topografic, atinge starea de echilibru limită (accelerație critică Kc) și, în același timp, permite calcularea factorului de siguranță obținut la fel ca și pentru celelalte metode comune din geotehnică.
Este o metodă bazată pe principiul echilibrului limită și al fâșiilor. Este considerat echilibrul unei mase de teren în alunecare împărțita în n fâșii verticale de grosime suficient de mică pentru a considera admisibilă presupunerea că efortul normal Ni acționează în punctul mediu al bazei fâșiei.
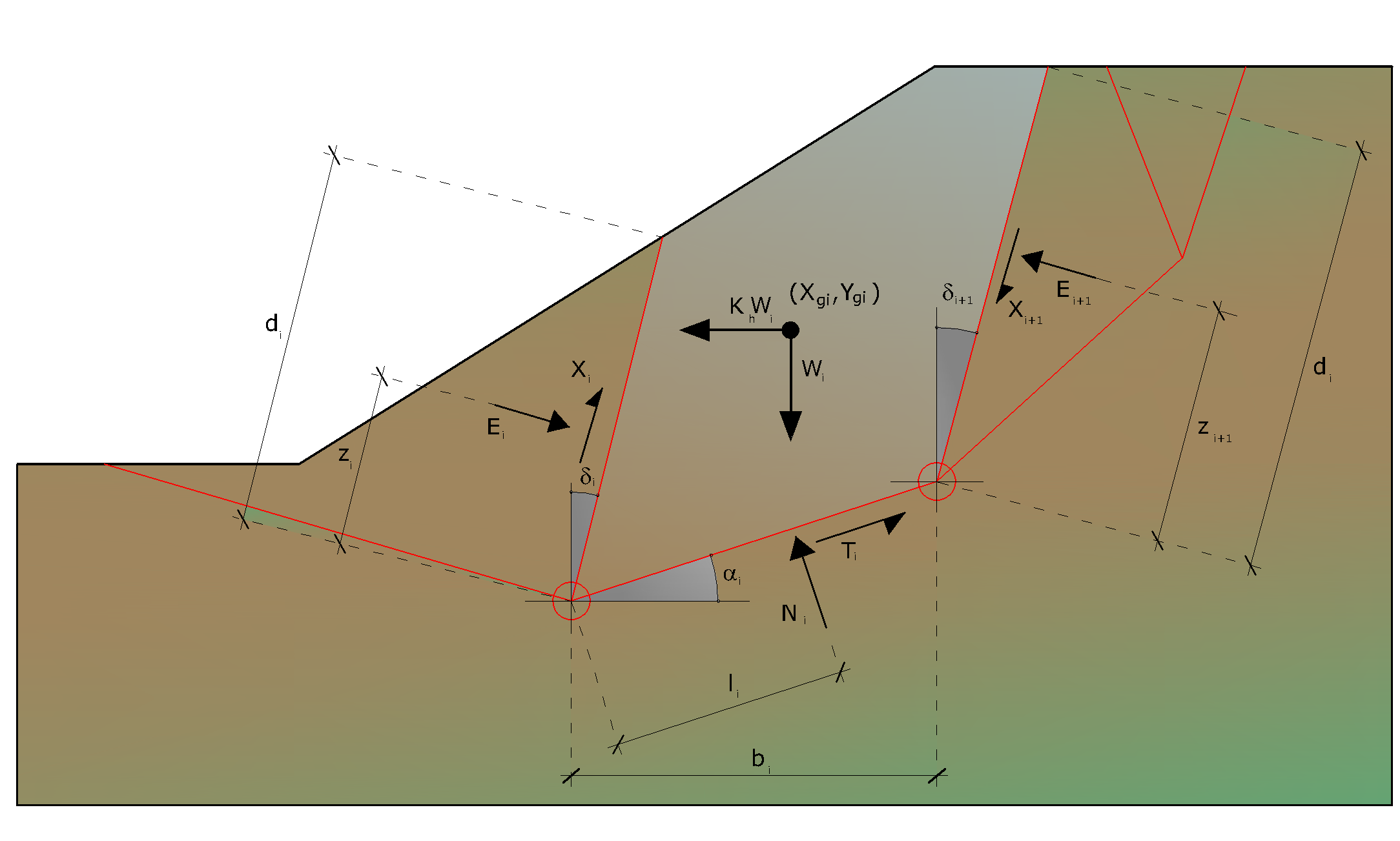
Acțiuni pe fâșia i conform teoriei lui Sarma
Ecuațiile de luat în considerare sunt:
- Ecuația echilibrului la deplasarea orizontală a fâșiei;
- Ecuația echilibrului la deplasarea verticală a fâșiei;
- Ecuația echilibrului momentelor.
Condiții de echilibru la deplasarea orizontală și verticală:
Ni cos αi + Ti sin αi = Wi - ΔXi
Ti cos αi - Ni sin αi = KWi +ΔEi
Se presupune că în absența forțelor externe pe suprafața liberă avem:
ΣΔEi = 0
ΣΔXì = 0
Unde Eì și Xi reprezintă forțele orizontale și respectiv verticale pe fața i a fâșiei generice i.
Ecuația echilibrului momentelor este scrisă alegând ca și punct de referință baricentrul întregului corp; astfel, după ce s-au parcurs o serie de poziții și transformări trigonometrice și algebrice, în metoda Sarma soluția problemei vine din rezolvarea a două ecuații:
![]()
Rezolvarea impune găsirea valorii K (accelerație seismică) corespunzătoare unui anumit factor de siguranță; și în special, găsirea valorii accelerației K ce corespunde factorului de siguranță F = 1 , sau accelerația critică.
Avem:
- K = Kc accelerația critică dacă F = 1
- F = Fs factorul de siguranță în condiții statice dacă K = 0
Cea de-a doua parte a problemei metodei Sarma constă în găsirea unei distribuții de forțe interne Xi și Ei astfel încât să verifice echilibrul fâșiei și cel global al întregului corp, fără încălcarea criteriului de cedare.
S-a constatat că o soluție acceptabilă a problemei se poate obține luând în calcul următoarea distribuție pentru forțele Xi:
![]()
unde Qi este o funcție cunoscută, în care se iau în considerare parametrii geotehnici medii pe fața i a fâșiei i, iar λ reprezintă o necunoscută.
Soluția completă a problemei se obține cu ajutorul valorilor Kc, l și F, care permit și obținerea distribuției forțelor dintre fâșii.
© GeoStru