Zeng și Liang au efectuat o serie de analize parametrice pe un model bidimensional dezvoltat cu un cod în elemente finite, ce reproduce cazul piloților imerși într-un teren în mișcare (drilled shafts). Modelul bidimensional reproduce o fâșie de teren de grosime unitară și presupune că fenomenul survine în condiții de deformare plană în directe paralelă cu axa piloților. Modelul a fost utilizat pentru a cerceta influenta în formarea efectului arc a anumitor parametrii ca interax între piloți, diametrul și forma piloților și proprietățile mecanice ale terenului. Autorii identifică în raportul dintre interax și diametrul piloților (s/d) parametru adimensional determinant pentru formarea efectului arc.
Problema este static nedeterminată, cu grad de nedeterminare egal cu (8n-4), dar cu toate acestea se poate abține o soluție reducând numărul necunoscutelor și considerând deci ipoteze simplificație, astfel încât să facă problema determinată.
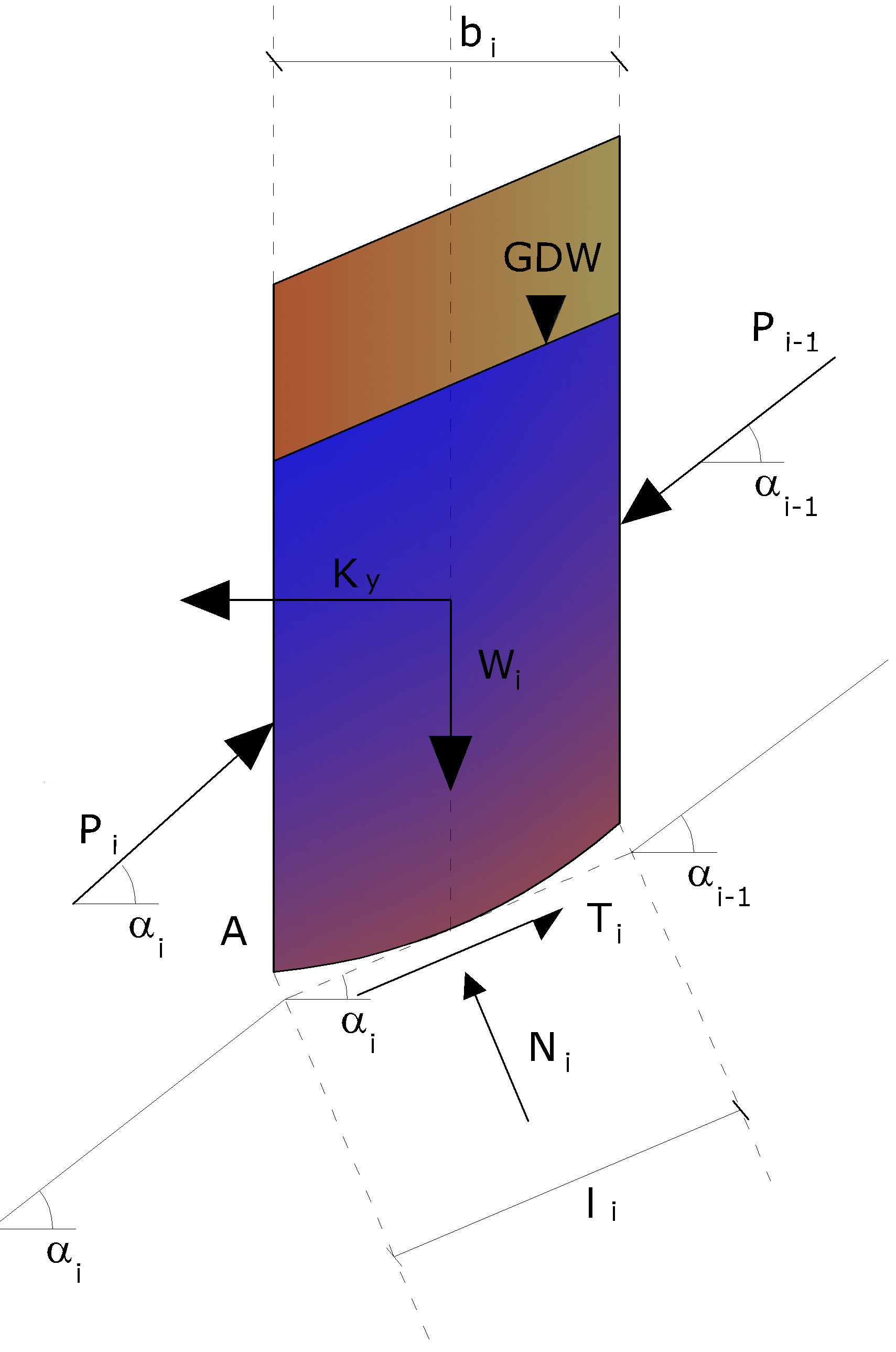
Acțiuni pe fâșia i conform teoriilor lui Zeng și Liang
Presupunerile care fac problema determinată sunt:
-Ky sunt luate ca orizontale pentru a reduce numărul total de necunoscute cu (n-1) la (7n-3)
-Forțele normale la baza fâșiei acționează în punctul mediu, reducând necunoscutele cu n la (6n-3)
-Poziția împingerilor laterale și la o treime din înălțimea medie a distanței dintre fâșii reduce necunoscutele cu (n-1) la (5n-2)
-Forțele (Pi-1) și Pi se iau paralele la înclinația bazei fâșiei (αi), reducând numărul necunoscutelor cu (n-1) la (4n-1)
-Se ia o singură constantă de curgere pentru toate fâșiile, reducând necunoscutele cu (n) la (3n-1)
Numărul total de necunoscute este redus astfel la (3n), de calculat folosind factorul de transfer de sarcină. Se ține cont de faptul că forța de stabilizare transmisă pe teren aval de piloți este redusă cu o cantitate R, numită factor de reducere, ce se calculează ca:
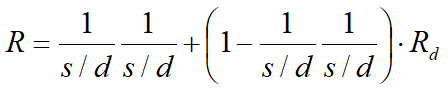
Factorul R depinde deci de raportul dintre interaxul prezent între piloți, diametrul piloților și factorul Rp ce ține cont de efectul arc.
© GeoStru